Topolojide sabit noktalar
Topolojide bir sabit nokta, bir fonksiyonun etkisi altında konumu değişmeyen noktadır.
Daha açık bir ifadeyle, elimizde bir f(x) fonksiyonu varsa, p noktası için f(p) = p eşitliği sağlanıyorsa, p bir sabit noktadır. Yani fonksiyon, p noktasında uygulandığında girdisiyle aynı sonucu verir.
$$ f(p) = p $$
Bir nesneyi merkez noktası P etrafında döndürdüğünü hayal et.
Bu dönüş, nesnedeki diğer noktaların uzaydaki koordinatlarını değiştirir; ancak merkez noktası P’nin konumu sabit kalır.
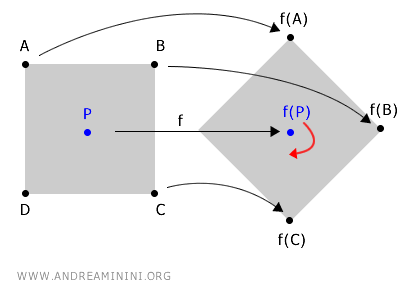
Bu durumda, dönüşün merkezi olan P noktası, fonksiyonun dönüş etkisi altında koordinatları değişmediği için bir sabit nokta olarak tanımlanır.
$$ f(P) \longrightarrow P $$
Sabit noktalar; sayısal analiz, oyun teorisi ve ekonomi gibi pek çok matematiksel alanın yanı sıra uygulamalı bilimlerde de temel bir kavramdır.
Topolojideki en bilinen örneklerden biri Brouwer’in Sabit Nokta Teoremi’dir.
Somut bir örnek
Kapalı [0, 2π] aralığında tanımlı f(x) = sin(x) fonksiyonunu ele alalım.
$$ f(x) = \sin(x) $$
p=0 radyan noktasında fonksiyonun sabit noktası kolayca görülebilir, çünkü sin(0) = 0’dır.
$$ \sin(0) = 0 $$
Burada fonksiyonun çıktısı, girdisiyle tamamen aynıdır.
Örnek 2
Şimdi aynı aralıkta tanımlı f(x) = cos(x) fonksiyonunu inceleyelim.
$$ f(x) = \cos(x) $$
Bu durumda x=0 bir sabit nokta değildir; çünkü cos(0) = 1’dir. Bu da giriş ve çıkış değerlerinin farklı olduğunu gösterir.
f(x) = cos(x) fonksiyonunun sabit noktası yaklaşık olarak x = 0.73908513 değerindedir.
$$ \cos(0.73908513) = 0.73908513 $$
Yani cos(0.73908513) değeri neredeyse tam olarak 0.73908513’tür.
Brouwer’in Sabit Nokta Teoremi
Bu önemli teorem şu şekilde ifade edilir:
n boyutlu kapalı bir uzayı sürekli olarak kendi üzerine eşleyen her fonksiyon en az bir sabit nokta içerir.
Bu bir varlık teoremidir; sabit noktanın en az bir tane olacağını garanti eder, ancak konumunu tam olarak belirtmez.
Bu ilke, özellikle dinamik sistemlerde ve ekonomik modellerde denge durumlarının varlığını ispatlamak açısından büyük önem taşır.
Ve benzeri durumlar için de geçerlidir.