Clopen Kümeler Nedir?

Bir küme, bulunduğu topolojide hem açık hem de kapalıysa, ona clopen küme denir.

Yani bu tür kümeler, aynı anda iki özelliği birden taşır: hem açık olma koşulunu hem de kapalı olma koşulunu sağlar.

"Clopen" kelimesi, İngilizce "closed" (kapalı) ve "open" (açık) sözcüklerinin birleşiminden gelir. Bu bileşik ad, aslında kavramın özünü çok güzel anlatır.

Clopen kümeler, hem açık kümelerin hem de kapalı kümelerin özelliklerini bir arada taşır. Böyle bir durum, bir küme ile onun tümleyeninin topolojide açık olduğu zaman ortaya çıkar.

Not: Gerçek sayılar kümesinde clopen kümelere pek rastlanmaz, ancak bazı özel topolojik uzaylarda oldukça önemli bir rol oynarlar. Çünkü bu kümeler, topolojik yapının nasıl "çalıştığını" anlamamızı kolaylaştırır.

Somut Bir Örnek

Şimdi küçük bir örnekle konuyu daha somut hale getirelim. Diyelim ki elimizde \(X=\{a,b,c,d\}\) kümesi ve buna ait bir topoloji \(T\) var.

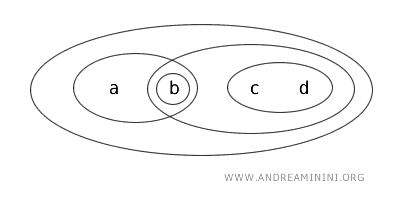
Bu topolojide açık kümeler şunlardır: \(\{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, \{a,b,c,d\}, \varnothing\).

Buradan, \(\{a,b\}\) alt kümesinin açık küme olduğunu görebiliriz.

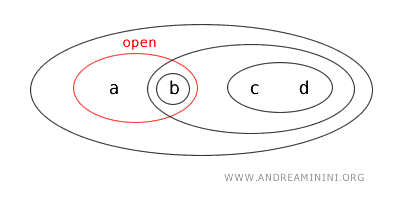
Fakat dikkat edelim: \(\{a,b\}\) kümesi aynı zamanda \(\{c,d\}\) kümesinin tümleyenidir.

$$ X - \{ c,d \} = \{a , b \} $$

Açık bir kümenin tümleyeni her zaman kapalı bir küme olduğuna göre...

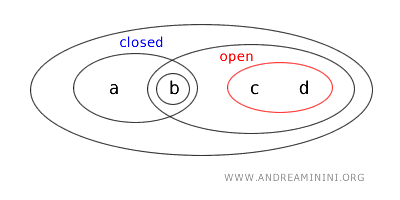
... \(\{a,b\}\) kümesinin aynı zamanda bir kapalı küme olduğunu da söyleyebiliriz.

Yani \(\{a,b\}\) hem açık hem de kapalıdır: başka bir deyişle, bu küme bir clopen kümedir.

Boş Küme ve Tüm Küme Her Zaman Clopen'dir

Topolojide istisnasız her zaman boş küme (\(\varnothing\)) ve tüm küme (\(X\)) clopen'dir - çünkü ikisi de hem açık hem de kapalıdır.

Bunu anlamak için açık ve kapalı kümelerin tanımlarını kısaca hatırlayalım:

• Boş küme (\(\varnothing\))
  Topolojinin temel aksiyomlarına göre boş küme daima açıktır. Aynı zamanda kapalıdır, çünkü tümleyeni \(X \setminus \varnothing = X\) (tüm küme) açıktır. Yani boş küme hem açık hem de kapalıdır.
• Tüm küme (\(X\))
  Tüm küme tanım gereği açıktır. Aynı zamanda kapalıdır, çünkü tümleyeni \(X \setminus X = \varnothing\) (boş küme) açıktır. Bu yüzden tüm küme de clopen'dir.

Sonuç olarak, her topolojik uzayda hem boş küme hem de tüm küme clopen kümelerdir.

Bu basit ama güçlü fikir, topolojinin temel taşlarından biridir ve daha karmaşık uzayları anlamamız için önemli bir başlangıç noktası oluşturur.