Topolojinin Tabanı

Topolojinin tabanı, bir topolojik uzay \( T \)’deki her açık kümenin, taban kümesi \( B \)’de yer alan açık kümelerin birleşimi olarak ifade edilebildiği açık kümeler ailesidir.

Eğer \( X \) bir küme ve \( X \)’in altkümelerinden oluşan, \( X \) üzerinde bir topoloji tanımlayan \( T \) ailesi verilmişse, bu topolojinin tabanı olan \( B \) kümesi, taban elemanları denilen kümelerden oluşur ve şu koşulları sağlar:

• \( X \)’teki her bir \( x \) elemanı mutlaka \( B \)’de bulunan en az bir kümeye ait olmalıdır.
• \( X \)’teki bir \( x \) elemanı, \( B \)’ye ait iki kümenin boş olmayan kesişimi \( B_1 \cap B_2 \) içinde bulunuyorsa, bu kesişim içerisinde \( x \)’i kapsayan başka bir \( B_3 \) kümesi bulunmalıdır. Yani \( x \), bir taban elemanı tarafından kapsanmalıdır.
  

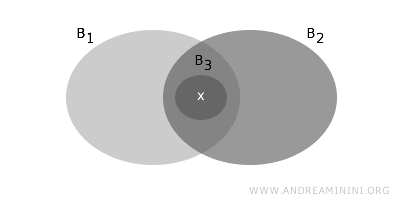
Bu koşullar, \( B \) ailesinin \( T \) topolojisi için bir taban oluşturmasını garanti eder.

Neden Önemlidir?

Topolojinin tabanı, \( T \) topolojisini yalnızca taban elemanlarının birleşimleri aracılığıyla tanımlamamıza olanak tanır. Böylece \( T \)’deki tüm açık kümeleri tek tek belirtmeye gerek kalmaz.

Not. Taban elemanlarının kesişimlerine ilişkin bu özellik, topolojinin temel aksiyomlarının sağlanmasını güvence altına alır. Özellikle, iki açık kümenin kesişiminin yine açık olmasını garanti eder.

Uygulamalı Bir Örnek

\( X \) kümesini ele alalım:

$$ \{ a, b, c \} $$

ve \( T \) topolojisini:

$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$

Bu durumda \( T \), \( X \) üzerindeki tüm açık kümeleri temsil eder ve tanım gereği her elemanı açıktır.

Bu topoloji için bir taban \( B \) şu şekilde tanımlanabilir:

$$ B = \{ \{ a \}, \{ b,c \} \} $$

Bu taban, gerekli tüm koşulları sağlar; çünkü \( X = \{ a,b,c \} \) kümesindeki her eleman \( B \)’deki en az bir kümeye aittir ve kesişim durumu söz konusu değildir.

\( T \)’deki her açık küme, \( B \)’deki kümelerin birleşimiyle ifade edilebilir.

Örneğin, {a} kümesi zaten \( B \)’de yer alır; {b,c} kümesi de \( B \)’dedir. Tüm uzay \( X \) ise {a} ile {b,c} kümelerinin birleşimiyle elde edilir:

$$ \{ a \} \in B $$

$$ \{ b,c \} \in B $$

$$ \{ a,b,c \} = \{ a \} \cup \{ b,c \} $$

Not. Küme teorisinde, boş küme \( \emptyset \), herhangi bir kümenin uygunsuz altkümesi olarak tanımlanır ve tanım gereği her zaman dahil edilir. Bu nedenle \( B \)’de de yer alır: $$ \emptyset \in B $$ Ayrıca boş küme, topolojide tanım gereği her zaman açık bir kümedir.

Bu örnek, sonlu bir durumda açık küme kavramının nasıl çalıştığını açıkça gösterir.

Daha karmaşık ya da sonsuz durumlarda taban kavramının tanımı ve kullanımı daha gelişmiş hale gelebilir; ancak temel fikir aynıdır: bir taban, topolojik uzaydaki tüm açık kümelerin “yapı taşlarını” oluşturur.

Alternatif Bir Yaklaşım

\( X = \{ a,b,c \} \) kümesi üzerindeki topoloji için alternatif bir taban \( B \) şu şekilde tanımlanabilir:

$$ B = \{ \{ a \}, \{ b \}, \{ c \} \} $$

Bu durumda taban, \( X \)’in tekil elemanlarından oluşur.

Bu, \( B \)’nin gerçekten de \( T = \{ \emptyset, X, \{ a \}, \{ b,c \} \} \) topolojisinin bir tabanı olduğunu doğrular.

• Boş küme \( \emptyset \), tanım gereği açık bir kümedir ve oluşturulması için eleman gerekmez. Ayrıca her kümenin uygunsuz altkümesidir ve her zaman dahil edilir.
• \{a\} kümesi zaten \( B \)’de yer alır. $$ \{ a \} \in B $$
• \{b,c\} kümesi, \( B \)’de bulunan \{b\} ve \{c\} kümelerinin birleşiminden elde edilir. $$ \{ b,c \} = \{ b \} \cup \{ c \} $$
• Tüm küme \( X = \{ a,b,c \} \), \( B \)’deki \{a\}, \{b\} ve \{c\} kümelerinin birleşimiyle elde edilir. $$ \{ a,b,c \} = \{ a \} \cup \{ b \} \cup \{ c \} $$

Dolayısıyla \( B \), \( X \) üzerindeki topolojinin bir tabanı olarak kabul edilir; çünkü \( T \)’deki tüm açık kümeler, \( B \)’deki kümelerin birleşimiyle oluşturulabilir.

Not. Bu örnek, aynı topoloji için birden fazla taban olabileceğini gösterir. Her biri, topolojideki açık kümeleri tanımlamak için geçerli bir yap

Sayılabilir Taban

Bir topolojinin sayılabilir tabanı, \( \mathcal{B} = \{B_1, B_2, B_3, \dots\} \) biçiminde sayılabilir bir açık kümeler ailesidir. Uzay \( X \)'teki her açık küme, bu ailedeki kümelerin birleşimi olarak ifade edilebilir.

Bir küme, eğer sonlu sayıda elemana sahipse ya da elemanları doğal sayılar kümesi \( \mathbb{N} \) ile birebir eşlenebiliyorsa, "sayılabilir" olarak adlandırılır.

Başka bir deyişle, bir küme veya aile, elemanları \( B_1, B_2, B_3, \dots \) biçiminde sıralanabiliyorsa, sayılabilir demektir.

Temel ile Sayılabilir Taban Arasındaki Fark

Her taban bir topoloji üretir; ancak yalnızca "sayılabilir" sayıda kümeye sahip olanlar, yani elemanları doğal sayılarla sıralanabilenler, sayılabilir taban olarak adlandırılır.

Neden Önemlidir? Bir topolojinin sayılabilir bir tabana sahip olması oldukça önemli bir özelliktir. Örneğin, bu durum Urysohn'un Metriğe Dönüştürülebilirlik Teoremi'nin koşullarından biridir. Ayrıca analiz ve topolojideki birçok temel sonuç yalnızca sayılabilir tabana sahip uzaylarda geçerlidir veya bu tür uzaylarda çok daha kolay biçimde incelenebilir.

Örnek

Standart topolojiye sahip \( \mathbb{R} \) uzayında, uç noktaları \( a, b \in \mathbb{Q} \) (rasyonel sayılar) ve \( a < b \) olan açık aralıkların \( (a, b) \) oluşturduğu aile, sayılabilir bir tabandır.

Çünkü bu aralıkların tümü sıralanabilir: \( I_1, I_2, I_3, \dots \) biçiminde etiketlenebilirler.

İspat

Doğal sayılar kümesi sayılabilirdir, çünkü elemanları şu şekilde sıralanabilir:

\[ 1, 2, 3, 4, 5, \dots \]

Eğer uç noktaları rasyonel olan ve \( a < b \) koşulunu sağlayan tüm aralıkları da benzer biçimde sıralayabiliyorsak, bu aralıkların kümesi de sayılabilir olur.

Rasyonel sayılar sonsuzdur ama sayılabilirdir. Örneğin şöyle sıralanabilirler:

\[ 0,\ 1,\ -1,\ \tfrac{1}{2},\ -\tfrac{1}{2},\ \tfrac{2}{3},\ -\tfrac{2}{3},\ \dots \]

Bu sayıları \( q_1, q_2, q_3, \dots \) olarak adlandıralım.

Şimdi \( q_i < q_j \) olacak şekilde tüm çiftleri \( (q_i, q_j) \) ele alalım.

Örneğin:

• \( (q_1, q_2) = (0, 1) \)
• \( (q_3, q_2) = (-1, 1) \)
• \( (q_4, q_5) = (\tfrac{1}{2}, -\tfrac{1}{2}) \) ❌ geçersizdir çünkü \( a > b \)
• \( (q_5, q_1) = (-\tfrac{1}{2}, 0) \)
• ...

Her geçerli çift (yani \( a < b \) koşulunu sağlayanlar) bir açık aralık tanımlar.

Bu aralıkları sıralayabiliriz:

1. \( (0, 1) \)
2. \( (-1, 1) \)
3. \( (-\tfrac{1}{2}, 0) \)
4. \( (0, \tfrac{1}{2}) \)
5. \( (-1, \tfrac{1}{2}) \)
6. \( (\tfrac{1}{2}, 1) \)
7. \( (-\tfrac{2}{3}, 0) \)
8. \( (0, \tfrac{2}{3}) \)
9. \( (-1, \tfrac{2}{3}) \)
10. \( (-\tfrac{1}{2}, \tfrac{1}{2}) \)
11. ...

Kısacası, bu tür aralıklar sonsuz sayıda olsa bile doğal sayılar gibi sıralanabilirler. İşte bu, bir kümenin sayılabilir olması anlamına gelir.

Dolayısıyla uç noktaları rasyonel olup \( a < b \) koşulunu sağlayan tüm aralıkların kümesi sayılabilir bir kümedir. Çünkü elemanları eksiksiz biçimde sıralamak mümkündür - tıpkı 1, 2, 3, … dizisinde olduğu gibi.

Gözlemler

Topolojinin tabanına ilişkin bazı ek gözlemler:

• Bir \( X \) kümesini ele alalım. Eğer her \( x \in X \) elemanının \(\{x\}\) biçiminde bir küme olarak \( B \)'de bulunduğu bir taban oluşturursak, bu taban yardımıyla \( X \) üzerinde bir topoloji \( T \) tanımlayabiliriz.

  Bu durumda tekil kümelerin birleşimiyle herhangi bir topoloji oluşturmak mümkündür.
  
  Örneğin \( X = \{a,b,c\} \) kümesi için \( B = \{\{a\}, \{b\}, \{c\}\} \) tabanı, \( T = \{\emptyset, \{a\}, \{b,c\}, X\} \) topolojisini üretir.
  
  Aynı taban \( B \), \( X \) üzerinde farklı topolojiler de oluşturabilir: örneğin \( T = \{\emptyset, \{b\}, \{a,c\}, X\} \), önemsiz topoloji \( T = \{\emptyset, X\} \) veya ayrık topoloji \( T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a,b\}, \{a,c\}, \{b,c\}, X\} \) gibi.

  Not. İlk koşul sağlanır çünkü \( X \)'in her elemanı \( B \)'deki bir kümeye dahildir. İkinci koşul da sağlanır çünkü \(\{x\}\) kümeleri tanım gereği birbirinden ayrıdır ve her biri yalnızca bir eleman içerir.

Bu gözlemler, topolojik yapıların tabanlarının farklı biçimlerde kurulabileceğini ve her birinin aynı uzayda farklı topolojiler doğurabileceğini gösterir.