Kapalı Kümeler
Bir topolojik uzay \( X \) içindeki \( B \) kümesi, eğer tamamlayıcısındaki her eleman \( u \in X - B \) için tamamen bu tamamlayıcının içinde kalan bir komşuluk bulunuyorsa, kapalı bir kümedir.
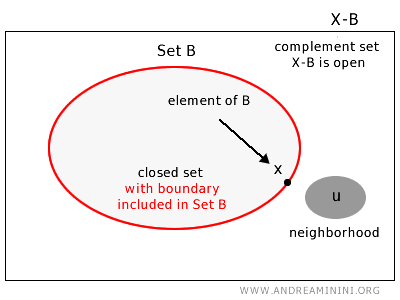
Kısacası, bir küme sınır noktalarının tümünü içeriyorsa kapalıdır.
Daha net söylemek gerekirse, bir topolojik uzay \( X \)’teki \( B \) kümesi, tamamlayıcısı \( X - B \) açık olduğunda kapalı olarak kabul edilir.
Not: Bu tanım, \( B \) kümesinde öyle noktalar bulunduğunu gösterir ki, bu noktaların çevresinde tamamen \( B \)’nin içinde kalan bir komşuluk bulunmaz.
Basit bir örnekle başlayalım
Gerçek sayı doğrusu \( \mathbb{R} \)’yi ve kapalı bir aralığı düşünelim.
Kapalı aralık nedir? \( \mathbb{R} \)’deki kapalı bir aralık, \( a \leq x \leq b \) koşulunu sağlayan tüm \( x \) değerlerinden oluşur. Burada \( a \) ve \( b \) gerçek sayılardır ve her iki uç nokta da kümeye dahildir.
Kapalı aralıklar genellikle \([a,b]\) şeklinde yazılır; köşeli parantezler, uç noktaların kümeye ait olduğunu belirtir.
Örneğin, \([3,10]\) aralığı gerçek sayı doğrusu \( \mathbb{R} \)’de kapalı bir kümedir.
Yani \( 3 \leq x \leq 10 \) koşulunu sağlayan her nokta, \( x=3 \) ve \( x=10 \) dâhil olmak üzere, bu kümeye aittir.
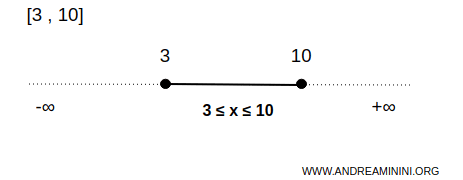
Ancak, uç noktalarda tamamen aralık içinde kalan bir komşuluk bulunmaz. Örneğin, \( x=3 \)’ün çevresinde alınacak her komşuluk, mutlaka 3’ten küçük bazı noktaları içerir ve bu noktalar aralığın dışında kalır.
Not: Sonsuz küçük bir komşuluk düşünsek bile, örneğin \( 3 \pm 0.00000001 \), bu komşuluk tamamen \([3,10]\) içinde değildir, çünkü \( 3 - 0.00000001 < 3 \)’tür. Benzer şekilde, \( x=10 \)’un etrafında da böyle bir komşuluk bulunmaz.
Bu, tek boyutlu bir kapalı küme için basit ama öğretici bir örnektir.
Kapalı küme kavramını genişletelim
Aynı fikir düzlemde de geçerlidir (\(\mathbb{R}^2\)).
Merkezi orijinde \((0,0)\) ve yarıçapı \( r=1 \) olan bir diski ele alalım:
$$ x^2 + y^2 \leq 1 $$
Bu eşitsizlik, merkezden uzaklığı 1 veya daha küçük olan tüm noktaları tanımlar. Yani hem diskin içindeki hem de çember üzerindeki noktalar kümenin bir parçasıdır.
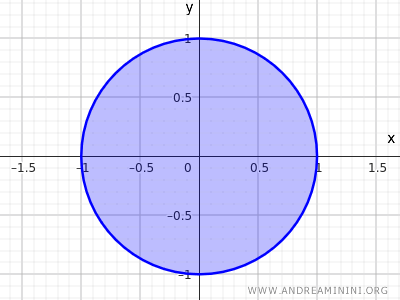
Dolayısıyla bu da kapalı bir kümedir.
Ancak dikkat edersek, \( x^2 + y^2 = 1 \) çemberi üzerindeki noktaların etrafında tamamen diskin içinde kalan komşuluklar yoktur.
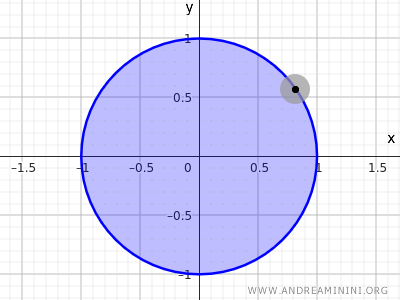
Not: \( x^2 + y^2 = 1 \) denklemiyle tanımlanan çember, öklidyen uzay \( \mathbb{R}^2 \)’de ne açık ne de kapalı bir kümedir, çünkü yalnızca çember üzerindeki noktaları içerir. Buna karşılık, \( x^2 + y^2 \leq 1 \) eşitsizliğiyle tanımlanan küme, hem iç noktaları hem de sınırı içerdiği için kapalıdır.
Benzer biçimde, bu kavram üç boyutlu uzayda katı bir küreye, daha genel olarak ise \( n \)-boyutlu uzayda kapalı bir \( n \)-küreye genişletilebilir.
Kapalı kümenin tümleyeni
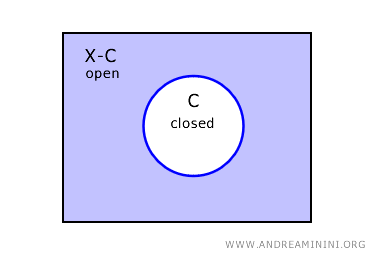
Bir topolojik uzay \( X \)’te kapalı bir küme \( C \)’nin tümleyeni, açık bir kümedir ve \( X - C \) ile gösterilir.
Yani \( C \) kapalıysa, tamamlayıcısı \( X - C \) zorunlu olarak açıktır.
Tersine, bir \( U \) kümesi açık ise, \( X - U \) kapalıdır.
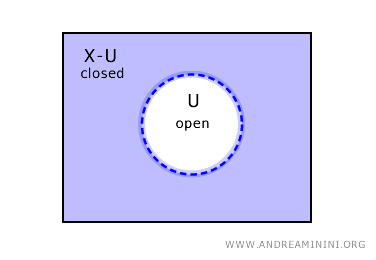
Fakat topolojide işler her zaman bu kadar basit değildir. Bazı topolojik uzaylarda hem açık hem de kapalı kümeler bulunduğu gibi, ne açık ne kapalı kümeler de vardır.
Dolayısıyla, bir kümenin kapalı olmaması onun açık olduğu anlamına gelmez; aynı şekilde açık olmaması da kapalı olmadığını göstermez.
Somut bir örnek
Topolojik bir uzay \( (X, T) \) düşünelim. Burada \( X = \{a,b,c,d\} \) dört elemandan oluşsun ve topoloji \( T \) aşağıdaki açık kümelerle tanımlansın:
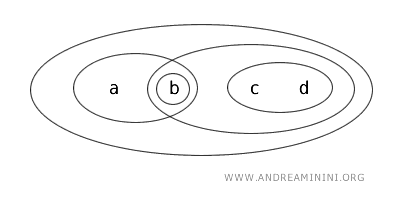
Açık kümeler şunlardır: \( \{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, X \) ve boş küme \( \varnothing \).
Şimdi bazı özel durumlara bakalım:
- \( \{b\} \) açık bir kümedir, çünkü topolojide açık olarak tanımlanmıştır.
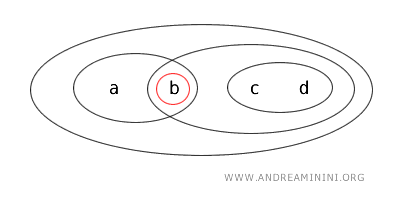
- \( \{a\} \) kapalı bir kümedir, çünkü tamamlayıcısı \( X - \{a\} = \{b,c,d\} \) açık bir kümedir.
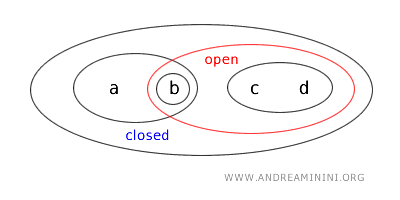
- \( \{a,b\} \) hem açık hem kapalıdır (clopen). Öklidyen topolojilerde bu durum pek sık görülmez, fakat genel topolojik uzaylarda mümkündür. Çünkü \( \{a,b\} \) açık olarak tanımlanmıştır ve tümleyeni \( \{c,d\} \) de açık olduğundan kapalıdır.
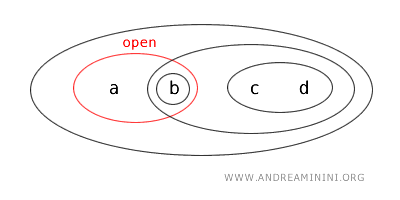
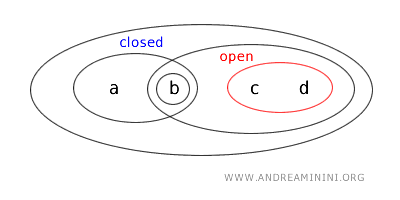
- \( \{b,c\} \) ne açık ne de kapalıdır, çünkü hem kendisi hem de tamamlayıcısı açık kümeler arasında yer almaz.
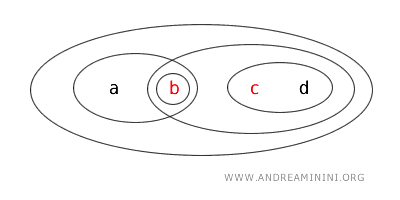
Bu örnek, topolojide bir kümenin açık, kapalı, her ikisi (clopen) veya hiçbirisi olabileceğini açıkça gösterir.
Kapalı kümelerin temel özellikleri
Kapalı kümeler, açık kümelerin tamamlayıcısı olarak tanımlanır. Bu kümelerin temel özellikleri şunlardır:
- Boş küme (\(\varnothing\)) ve tüm uzay \( X \) her zaman kapalıdır.
- Kapalı kümelerin herhangi bir (sonlu veya sonsuz) kesişimi yine kapalıdır.
- Sonlu sayıda kapalı kümenin birleşimi de kapalı bir kümedir.
Ek bir örnek
\( \mathbb{R}^n \) uzayının standart topolojisinde her nokta kapalı bir kümedir.
Gerçek sayı doğrusu (\( \mathbb{R}^1 \)) üzerindeki bir \( n \) noktasını ele alalım. Tümleyeni, \( n \) dışındaki tüm noktaları içerir.
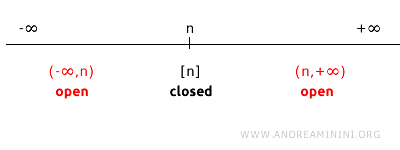
\(\{n\}\)’nin tümleyeni iki açık aralığın birleşimidir: \((-\infty, n) \cup (n, +\infty)\). Bu aralıklar açık olduğundan, birleşimleri de açık bir kümedir. Dolayısıyla \(\{n\}\) kapalı bir kümedir.
Ancak her topolojide bu durum geçerli değildir. Örneğin, \( \mathbb{R} \)’de her tam sayı \( n \) için açık aralıklar \( (n, n+1) \) ile oluşturulan bir topoloji düşünelim. Bu topolojide tekil noktalar kapalı değildir, çünkü hiçbir açık kümenin tamamlayıcısı bu noktaları tam olarak vermez.
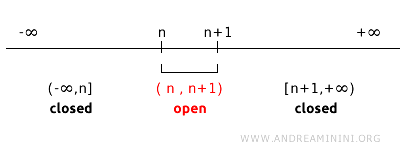
Bu durumda, kapalı küme kavramının uzayın topolojik yapısına bağlı olduğunu görürüz.
Son gözlemler
Örnek: Gerçek sayı doğrusundaki \([0,1]\) kapalı aralığını ele alalım. Bu küme, tüm yığılma noktalarını içerir.
Örneğin, \(0.5\) noktasının çevresinde alınacak herhangi bir açık aralık, \([0,1]\) içinden sonsuz sayıda nokta barındırır. Bu da \(0.5\)’in bir yığılma noktası olduğunu gösterir.
![[0,1] kapalı aralığındaki 0.5 noktasının yığılma noktası örneği](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-1.gif)
Aynı durum uç noktalar için de geçerlidir. \(0\) noktasının çevresinde alınacak her komşulukta, örneğin \(0.1, 0.01, 0.001\) gibi aralık noktaları bulunur. Bu yüzden \(0\) da bir yığılma noktasıdır.
![[0,1] kapalı aralığının uç noktaları yığılma noktalarıdır](/data/andreaminininet/closed-set-example-limit-point-am-net-2024-2.gif)
Dolayısıyla, \([0,1]\) aralığındaki tüm noktalar kümenin yığılma noktalarıdır.
- Kapalı Kümeler ve Yığılma Noktaları
Bir kümenin yığılma noktası, ne kadar küçük seçilirse seçilsin, komşuluğunda her zaman kümeden en az bir başka nokta bulunan noktadır. Bu özellik, kapalı kümeleri tanımlar; çünkü bir küme tüm yığılma noktalarını içeriyorsa kapalıdır. - Bir \( A \) kümesi ancak ve ancak \( A = \overline{A} \) olduğunda kapalıdır
Bir topolojik uzayda, \( A \) kümesi kapanışına eşitse, yani \( A = \overline{A} \), o zaman kapalıdır. \( A \)’nın kapanışı hem \( A \)’nın noktalarını hem de yığılma noktalarını içerir. Tanım gereği, bir küme tüm yığılma noktalarını kapsıyorsa kapalıdır.
Topolojideki bu kavram, uzayların yapısını anlamak için temel bir adımdır. Kapalı kümeler, süreklilik, limit ve kompaktlık gibi pek çok ileri konunun yapıtaşını oluşturur.