Bir Kümenin İçi

Bir topolojik uzay $ X $ içinde, bir küme $ A $’nın içi, $ A $ kümesi içerisinde bulunan tüm açık alt kümelerin birleşimidir. Genellikle $ \text{Int}(A) $ veya $ A^\circ $ sembolleriyle gösterilir.

Bir kümenin içi, $ A $’nın tamamen içinde yer alan en büyük açık alt kümeyi ifade eder.

$ A $ kümesi içerisinde, içten daha büyük bir açık alt küme bulunmaz.

Not: İçin doğası, tanım gereği açık alt kümelerin birleşimi olmasından gelir. Bu nedenle iç küme daima açık bir kümedir.

Resmî olarak, $ A $’nın içi, $ A $’daki her noktanın çevresinde tamamen $ A $ içinde kalan bir açık komşuluk bulunan noktaların tümü olarak tanımlanır.

$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ , } X \text{’te açık bir kümedir} \} $$

Başka bir deyişle, $ A $’nın içindeki her nokta $ x $ için, $ x $’i içeren ve bütünüyle $ A $’nın içinde kalan en az bir açık küme $ U $ vardır.

Unutulmamalıdır ki bir kümenin içi $A$, onu içeren topolojik uzay $X$’in yapısına bağlıdır; kümenin kendi özelliklerine değil. Dolayısıyla $ A $’nın içi, tanımlandığı topolojiye göre farklılık gösterebilir.

Uygulamalı Bir Örnek
Bir Kümenin İçi Teoremi
İç Kümenin Temel Özellikleri
Ek Notlar

Uygulamalı Bir Örnek

standart topoloji altında $ \mathbb{R} $ üzerinde tanımlı $ A = [0, 1] $ kümesini ele alalım.

Bu aralık, 0 ile 1 arasındaki tüm gerçek sayıları kapsar.

Bu durumda $ A $’nın içi $ (0, 1) $’dir.

$$ \text{Int}(A) = (0,1) $$

Bu, 0 ile 1 arasındaki noktaları içeren en büyük açık aralıktır. Uç noktalar olan 0 ve 1 dahil değildir, çünkü bu noktalar tamamen $ A $ içinde yer alan hiçbir açık aralığın parçası değildir.

Örnek 2

Şimdi, yine standart topoloji altında $ \mathbb{R} $ üzerinde $ A = [0, 1) $ kümesini inceleyelim.

Bu aralık, 0’dan (dahil) başlayıp 1’e kadar (hariç) uzanır. Yani sol uç kapalı, sağ uç açıktır.

Bu durumda da $ A $’nın içi, bir önceki örnekte olduğu gibi $ (0,1) $’dir:

\[ \text{Int}(A) = (0,1) \]

Bunun nedeni, topolojik uzaylarda iç kavramının, bir küme içinde tamamen yer alan tüm açık alt kümelerin birleşimiyle tanımlanmasıdır.

Not: $ \mathbb{R} $’de standart topoloji altında, açık aralıklar temel açık kümelerdir. Dolayısıyla $ [0,1) $ kümesinde yer alan en büyük açık alt küme $ (0,1) $’dir. Sol uç noktası 0 hiçbir açık aralığın tamamen içinde bulunmadığından dışlanır. Böylece $ (0,1) $, $ A $’nın içinde açık aralıklarla çevrelenebilen tüm noktaları içerir ve iç tanımını karşılar.

Örnek 3

Şimdi $ X $ üzerinde ayrık topoloji tanımlandığında $ A = [0,1) $ kümesini ele alalım.

Ayrık topolojiye sahip bir uzayda, $ X $’in her alt kümesi açık kabul edilir.

Bu durumda, $ A $’nın her elemanı, tamamen $ A $ içinde yer alan bir komşuluk tarafından çevrelenebilir. Bu komşuluk, $ A $’nın herhangi bir alt kümesinden oluşabilir.

Ayrık topolojiye sahip $ \mathbb{R} $’de her alt küme açık kabul edilir. Buna tüm açık ve kapalı aralıklar ile noktaların herhangi bir kombinasyonu dahildir. Örneğin $ (0,0.5) $, $ (0.25,0.75) $, $ (0,1) $ gibi açık aralıklar, $ [0,0.25] $ gibi kapalı aralıklar, boş küme ve tüm $ [0,1) $ aralığı açık kabul edilir.

Her alt küme açık olduğundan, $ A = [0,1) $ bu topoloji altında açık bir kümedir.

Dolayısıyla bu durumda $ A $’nın içi $ A $’nın kendisidir, çünkü $ A $’daki her nokta, o noktayı içeren ve tamamen $ A $ içinde kalan bir açık alt kümenin parçasıdır.

$$ \text{Int}(A) = A = [0,1) $$

Ayrık topolojide herhangi bir kümenin içi her zaman o kümenin kendisine eşittir.

Not: Bu örnek, seçilen topolojinin komşulukların ve iç kavramının özelliklerini nasıl etkilediğini gösterir. Daha önce belirtildiği gibi, bir komşuluğun özellikleri, kümenin tanımlandığı topolojik yapı $ X $’e bağlıdır.

Örnek 4

$ X = \{a, b, c\} $ noktalarından oluşan bir topolojik uzay düşünelim ve bu uzay üzerinde ayrık topoloji tanımlandığını varsayalım.

Bu durumda $ X $’in her alt kümesi açıktır:

Tanım gereği $ \emptyset $ ve $ \{a, b, c\} $ kümeleri $ X $’te açıktır.
$ \{a\} $, $ \{b\} $ ve $ \{c\} $ gibi tek elemanlı kümeler de açıktır, çünkü ayrık topolojide her nokta kendi başına açık bir kümedir.
$ \{a, b\} $, $ \{a, c\} $ ve $ \{b, c\} $ gibi iki elemanlı alt kümeler de açıktır, çünkü açık kümelerin birleşimleriyle elde edilirler.

$ X $ içinde $ A = \{b, c\} $ kümesini ele alalım:

Tanıma göre, $ \text{Int}(A) $, $ A $ içinde yer alan tüm açık alt kümelerin birleşimidir.

$ A $’nın açık alt kümeleri $ \{b\} $, $ \{c\} $ ve $ \{b, c\} $’dir.

\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]

Dolayısıyla bu açık kümelerin birleşimi $ \{b, c\} $’dir ve bu da tam olarak $ A $’ya eşittir.

Sonuç olarak $ \text{Int}(A) = A $ elde edilir.

Not: Bu sonuç yalnızca $ A $’ya özgü değildir; ayrık topolojiye sahip herhangi bir uzayda, her alt küme $ S \subseteq X $ için geçerlidir. Böyle bir uzayda her alt küme açık olduğundan, herhangi bir kümenin içi o kümenin kendisine eşittir, yani $ \text{Int}(S) = S $.

Bir Kümenin İçi Teoremi

Bir topolojik uzay $ X $'te, $ S \subseteq X $ bir alt küme ve $ y \in X $ bir eleman olmak üzere, $ y $ noktası $ S $'nin içi olan $ \text{Int}(S) $'ye aittir ancak ve ancak $ y $'yi içeren ve tamamen $ S $'nin içinde yer alan bir açık küme $ U $ varsa. Matematiksel olarak: $$ y \in \text{Int}(S) \iff \exists \, U \text{ açık, öyle ki } y \in U \subseteq S $$

Başka bir ifadeyle, bir nokta $ y \in X $, eğer $ S $'nin içinde tamamen yer alan bir açık küme $ U $'nun elemanıysa, $ S $'nin iç bölgesinde bulunur.

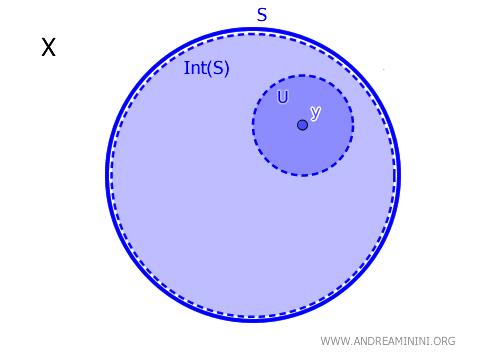
görsel örnek

Bu teorem, topolojik uzay $ X $'te bir nokta $ y $'nin, bir küme $ S $'nin içinde yer alıp almadığını belirlemek için gerekli ve yeterli koşulu ortaya koyar.

İspat

Gerekli koşul: Eğer $ y $, $ S $'nin içindeyse, yani $ y \in \operatorname{Int}(S) $, tanım gereği $ y $'yi içeren ve tamamen $ S $'nin içinde bulunan bir açık küme $ U $ vardır. Dolayısıyla, $ y $'nin içte olması bu tür bir $ U $'nun varlığını zorunlu kılar.
Yeterli koşul: Eğer $ y $'yi içeren ve $ S $'nin içinde tamamen yer alan bir açık küme $ U $ mevcutsa, o zaman $ U $'daki her nokta - dolayısıyla $ y $ de - $ S $'nin içindedir. Çünkü bir kümenin içi, $ S $'nin içinde yer alan tüm açık alt kümelerin birleşimi olarak tanımlanır. Bu nedenle $ y \in \operatorname{Int}(S) $ olur.

Not: Bu teorem, açık kümeler ile bir kümenin iç kavramı arasındaki bağı doğrudan kurar ve bu ilişki süreklilik, limit ve diğer temel topolojik kavramların anlaşılmasında merkezi bir öneme sahiptir.

Örnek

Standart topoloji altında $ \mathbb{R} $ üzerinde tanımlı $ A = [1,3] $ kümesini ele alalım.

$$ A = [1,3] $$

Bu aralık, 1 ile 3 arasındaki tüm gerçek sayıları içerir.

Şimdi, iç teoremini kullanarak $ A $'nın içini bulalım.

$ A $'nın içini belirlemek için, $ U \subseteq A $ olacak şekilde bir açık küme $ U $ bulmamız gerekir; öyle ki $ U $'daki her nokta $ \operatorname{Int}(A) $'ya da ait olsun.

$ U $'nun seçimi:
$ U = (1,3) $ açık aralığını seçelim. Bu küme, uç noktalar hariç 1 ile 3 arasındaki tüm noktaları içerir ve standart topoloji altında açık bir kümedir.
$ U \subseteq A $ koşulunun doğrulanması:
$ U = (1,3) $'teki her nokta $ A = [1,3] $'te de yer alır. Ancak uç noktalar $ 1 $ ve $ 3 $, açık küme tanımı gereği $ U $'ya dahil değildir.

Dolayısıyla $ U $, $ A $'nın içinde tamamen yer alan bir açık kümedir. Bu durumda $ A $'nın içi, yani $ \operatorname{Int}(A) $, tam olarak $ (1,3) $'tür.

Not: Bu örnek, $ A $'nın içinin açık aralık $ (1,3) $ olduğunu açıkça gösterir. Uç noktalar $ 1 $ ve $ 3 $, hiçbir açık aralığın tamamen $ A $'nın içinde bulunmaması nedeniyle $ \operatorname{Int}(A) $'ya dahil değildir.

İç Kümenin Temel Özellikleri

Bu bölümde, topolojik uzaylarda iç kavramıyla ilgili temel özellikler ele alınmaktadır. Bu özellikler, iç, kapanış, birleşim ve kesişim gibi topolojik işlemler arasındaki yapısal ilişkileri ortaya koyar.

İçlerin Birleşimi Özelliği
İki kümenin içlerinin birleşimi, bu kümelerin birleşiminin içinin bir alt kümesidir. Ancak bu içerme genellikle eşitlik sağlamaz: $$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
İçlerin Kesişimi Özelliği
İki kümenin içlerinin kesişimi, bu kümelerin kesişiminin içiyle tam olarak çakışır: $$ \text{Int}(A) \cap \text{Int}(B) = \text{Int}(A \cap B) $$
Tümleyenin İçi ile Kapanışın Tümleyeni Arasındaki İlişki
Bir kümenin tümleyenin içi, o kümenin kapanışının tümleyenine eşittir: $$ \text{Int}(X - A) = X - \text{Cl}(A) $$
Tümleyenin Kapanışı ile İçin Tümleyeni Arasındaki İlişki
Bir kümenin tümleyenin kapanışı, o kümenin içinin tümleyenine eşittir: $$ \text{Cl}(X - A) = X - \text{Int}(A) $$

Ek Notlar

Eğer U, X'te açık bir küme ve U ⊆ A ise, o zaman U ⊆ Int(A)
Eğer $ U $, topolojik uzay $ X $'te açık bir küme olup tamamen $ A $'nın içinde yer alıyorsa, $ U $ aynı zamanda $ A $'nın içinin bir alt kümesidir. Çünkü $ \text{Int}(A) $, $ A $'nın içinde yer alan en büyük açık kümedir.
Eğer A ⊆ B ise, o zaman Int(A) ⊆ Int(B)
Eğer $ A $ kümesi $ B $'nin alt kümesiyse, $ A $'nın içi de $ B $'nin içinin alt kümesidir. Çünkü $ A $'nın içinde bulunan her açık küme, aynı zamanda $ B $'nin içinde de yer alır. Dolayısıyla iç alma işlemi alt küme ilişkisini korur.
Bir küme A açıktır ⇔ A = Int(A)
Bir topolojik uzay $ X $'te bir küme $ A $, ancak ve ancak $ A = \text{Int}(A) $ eşitliği sağlandığında açık bir kümedir. Yani $ A $'daki her noktanın, tamamen $ A $'nın içinde yer alan bir açık komşuluğu varsa, $ A $ açık bir kümedir.
Bir kümenin içini hesaplamak için R programlama dili kullanılabilir
R dili, matematiksel ve istatistiksel hesaplamalar için güçlü bir araçtır. Bu nedenle, topolojik uzaylarda kümelerin içlerini hesaplamak ve bu kavramı analitik olarak incelemek için uygun bir ortam sunar.

ve benzeri açıklayıcı notlar.