A Kümesinin Sınırının A’nın Alt Kümesi Olması, A’nın Kapalı Olmasıyla Eşdeğerdir

Bir küme \( A \)’nın sınırı \( \partial A \), ancak ve ancak \( A \) kapalı bir küme olduğunda \( A \)’nın bir alt kümesidir. \[ \partial A \subseteq A \Leftrightarrow A \text{ kapalıdır} \]

Pratik Örnekler

Örnek 1

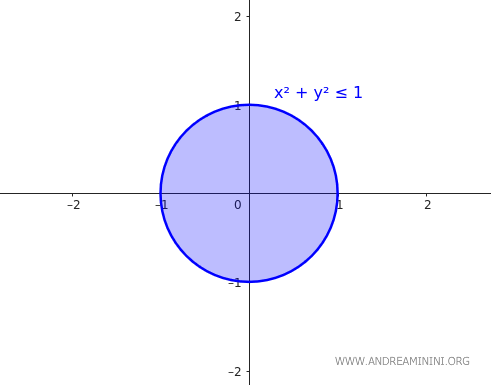
\( A \) kümesini, Öklid uzayı \(\mathbb{R}^2\)’de orijin merkezli ve yarıçapı 1 olan kapalı bir disk olarak ele alalım.

$$ A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 1 \} $$

Bu kümenin sınırı, yarıçapı 1 olan çemberden oluşur:

$$ \partial A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 = 1 \} $$

\( A \) kapalı bir küme olduğu için sınır üzerindeki tüm noktaları içerir. Başka bir ifadeyle, sınırın her noktası aynı zamanda \( A \)’nın bir elemanıdır:

$$ \partial A \subseteq A $$

Bu durum, \( A \)’nın kapalı bir küme olduğunu doğrudan doğrular.

Örnek 2

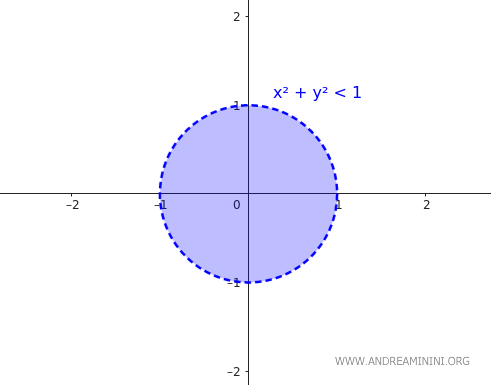
Şimdi \( B \) kümesini, yine orijin merkezli ve yarıçapı 1 olan açık bir disk olarak tanımlayalım:

$$ B = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 \} $$

\( B \)’nin sınırı da yine yarıçapı 1 olan çemberdir:

$$ \partial B = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 = 1 \} $$

Ancak \( B \) açık bir küme olduğundan, sınır noktalarını içermez. Bu nedenle:

$$ \partial B \nsubseteq B $$

Bu da \( B \)’nin kapalı bir küme olmadığını açık biçimde gösterir.

Bu iki örnek, kapalı ve açık kümeler arasındaki farkı net bir şekilde ortaya koyar: kapalı kümeler sınırlarını içerirken, açık kümeler içermez.

İspat

Şimdi bu sonucun neden doğru olduğunu iki adımda gösterelim.

1] A’nın Sınırı A’nın Alt Kümesiyse, A Kapalıdır

\( \partial A \subseteq A \) olduğunu, yani \( A \)’nın sınır kümesinin tamamen \( A \)’nın içinde yer aldığını varsayalım.

Hatırlatalım ki \( A \)’nın sınırı şu şekilde tanımlanır:

\( \partial A = \overline{A} \cap \overline{A^c} \)

Burada \( \overline{A} \), \( A \)’nın kapanışını; \( \overline{A^c} \) ise \( A \)’nın tümleyeninin kapanışını ifade eder.

Sınır tanımı gereği, \( \partial A \)’daki her nokta ya \( A \)’nın ya da \( A^c \)’nin bir yığılma noktasıdır.

Eğer sınırdaki tüm noktalar \( A \)’ya aitse, bu durum \( A \)’nın bütün yığılma noktalarını içerdiği anlamına gelir. Bu ise kapalı kümenin tanımıdır.

Dolayısıyla \( \partial A \subseteq A \) koşulu, \( A \)’nın kapalı olmasını zorunlu kılar.

2] A Kapalıysa, Sınırı A’nın Alt Kümesidir

Şimdi tersini varsayalım ve \( A \)’nın kapalı bir küme olduğunu kabul edelim.

Kapalı kümeler için kapanış, kümenin kendisine eşittir:

$$ A = \text{Cl}(A) $$

Bu durumda sınır tanımını kullanarak şunu yazarız:

$$ \partial A = \text{Cl}(A) \cap \text{Cl}(A^c) $$

\( \text{Cl}(A) = A \) olduğundan:

$$ \partial A = A \cap \text{Cl}(A^c) $$

Bu ifade, hem \( A \)’ya ait olan hem de \( A \)’nın tümleyeninin kapanışında yer alan noktaları gösterir. Bunlar tam olarak \( A \)’nın sınır noktalarıdır.

Dolayısıyla \( A \) kapalıysa, sınırı mutlaka \( A \)’nın bir alt kümesidir.

3] Sonuç

Sonuç olarak, bir kümenin sınırının kendisinin bir alt kümesi olması, o kümenin kapalı olmasıyla tam anlamıyla eşdeğerdir.

Ve devamı.