Topoloji

Topoloji, bir uzayın yırtılmadan ya da yapıştırılmadan, yalnızca esnetme, bükme ve eğme gibi sürekli deformasyonlar altında değişmeden kalan özelliklerini inceleyen matematik dalıdır.

Bu nedenle topoloji, bir dönüşümün sürekli olması koşuluyla korunan geometrik niteliklere odaklanır ve şekillerin görünüşünden çok yapısal özelliklerini ele alır.

Bu tür özellikler ancak süreksiz işlemlerle değişebilir; örneğin uzayın bir bölümünün yırtılması ya da iki ayrı bölümün birbirine yapıştırılması durumunda.

Örneğin bir küre ile bir küp topolojik olarak denktir, çünkü biri diğerine herhangi bir yırtma veya yapıştırma işlemi olmadan, tamamen sürekli bir deformasyonla dönüştürülebilir.

Buna karşılık bir küre ile bir torus topolojik olarak denk değildir; çünkü birini diğerine dönüştürmek, bir deliğin oluşturulmasını ya da ortadan kaldırılmasını gerektirir ve bu işlem kaçınılmaz olarak yırtma veya yapıştırmayı içerir.

Başka bir deyişle topoloji, uzayların nicel ölçülerinden çok, nasıl düzenlendikleri ve hangi biçimde birbirleriyle bağlantılı olduklarıyla ilgilenir.

Topolojik bir bağlamda uzunluk, alan, hacim ya da açı ölçüsü gibi kavramlar belirleyici değildir. Önemli olan, şekillerin niteliksel özellikleri ve sürekli deformasyonlar yoluyla birbirlerine dönüştürülüp dönüştürülemeyecekleridir.

Bu yaklaşım, örneğin bağlantılılık, kompaktlık, bir nesnenin sahip olduğu delik sayısı ve bir uzayın diğer küresel özelliklerini kapsar.

Topoloji, topolojik uzay kavramını tanımlar ve bu alandaki temel dönüşümler homeomorfizmlerdir; yani bir uzayı, topolojik yapısını koruyarak, sürekli ve tersinir bir biçimde başka bir uzaya eşleyen dönüşümlerdir.

Bu nedenle topoloji sıklıkla “lastik levha geometrisi” olarak nitelendirilir: nesneler esnek bir maddeden yapılmış gibi düşünülür ve gerilebilir, bükülebilir veya sıkıştırılabilirler, ancak yırtılamaz ya da yapıştırılamazlar. Bu yönüyle topoloji, modern matematiğin en temel ve aynı zamanda en birleştirici alanlarından biridir.

Tarihçe

Topolojinin temelleri 18. yüzyılda atılmıştır.

Kökeni, Leonhard Euler’in bağlantı ve ağ teorisinin temellerini atan Königsberg’in Yedi Köprüsü problemine dayanır.

Bu problem, uzayların yapısal özellikleri hakkında temel sorular doğurmuş ve topolojinin gelişiminin başlangıç noktası olmuştur.

Yedi Köprü problemi: Bir nehir adasında yedi köprü vardır. Başlangıç noktanız neresi olursa olsun, her köprüden tam bir kez geçmenizi sağlayacak bir yol mümkün müdür? Önemli olan, aynı köprüden ikinci kez geçilememesidir.

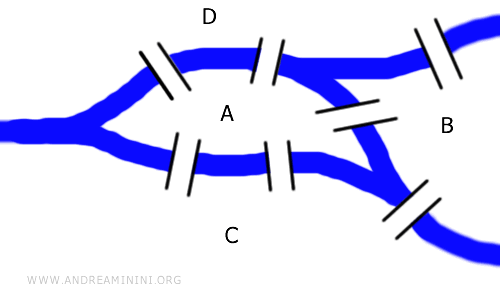
Bu sorunun çözümü için köprülerin uzunluklarını ya da aralarındaki mesafeleri bilmek gerekmez; mesele tamamen topolojiktir ve grafiklerle de temsil edilebilir. Buradaki grafik, köprülerin ilk düzeniyle topolojik olarak aynıdır.

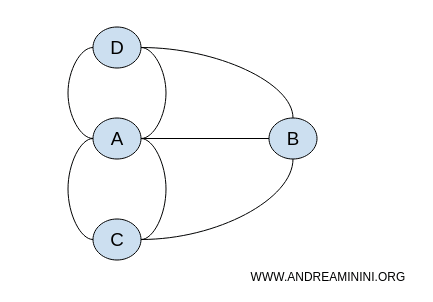
Grafikte düğümlerin kesin konumları önemli değildir. Önemli olan düğümler arasındaki bağlantılardır. Dolayısıyla problem, sonsuz sayıda farklı ama topolojik olarak eşdeğer grafikle ifade edilebilir.

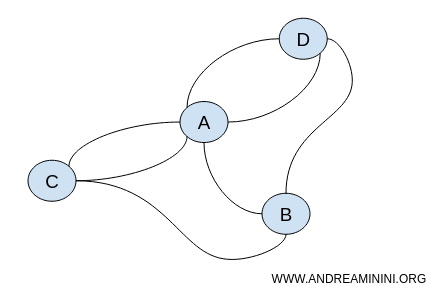
Her iki grafik de süreklilik ve bağlantı gibi aynı topolojik özellikleri korur.

Euler, Yedi Köprü probleminin geometrik görünüme sahip olsa da ölçümlerden bağımsız olduğunu fark etti.

Problemin aslında konumla ilgili olduğunu ve çözümsüz olduğunu gösterdi. Bu da “konum geometrisi” kavramını doğurdu.

19. yüzyıl boyunca Carl Friedrich Gauss, August Ferdinand Möbius, Johann Listing, Bernhard Riemann ve Felix Klein gibi matematikçiler şekillerin ve yüzeylerin özelliklerini inceleyerek topolojik kavramları daha da geliştirdiler.

Not: “Topoloji” terimini ilk kez Johann Listing 1847’de kullandı, ancak bilim çevrelerinde yaygınlaşması onlarca yıl aldı.

19. yüzyılda konum geometrisi, Gustav Kirchhoff’un elektrik ağları üzerine yaptığı çalışmalar gibi pratik alanlarda da uygulama buldu.

Daha sonra, 19. yüzyılın sonları ve 20. yüzyılın başlarında Henri Poincaré cebirsel topoloji çalışmalarıyla konum geometrisine büyük katkılar yaptı.

20. yüzyılda topoloji, özellikle soyut matematikte Felix Hausdorff, Cantor ve Brouwer gibi isimlerin katkılarıyla cebirsel topoloji ve genel topoloji gibi alt dallara ayrıldı.

Bugün topoloji, sürekli dönüşümler altında değişmeyen özellikleri inceleyen temel bir matematik alanıdır.

Topoloji artık cebirsel topoloji, diferansiyel topoloji, genel topoloji ve geometrik topoloji gibi birçok alt disiplini kapsamaktadır.

Genel bakıldığında topoloji, şekillerin yapısının genel incelenmesi; daha soyut düzeyde ise matematiğin teorik bir disiplini olarak görülebilir.

Soyut bir alan olmasına rağmen, topolojik kavramlar ekonomi, mühendislik ve fen bilimleri gibi birçok alanda gerçek problemlere uygulanabilmektedir.

Topolojik Uzaylar

Topolojik uzay, X kümesinin T adı verilen bir “topoloji” ile donatılmış hâlidir. Bu yapı, süreklilik, yakınlık ve limit gibi kavramların klasik geometri ve matematik analizden çok daha genel bir çerçevede ele alınmasını sağlar.

$$ (X,T) $$

Örnek: Topolojik uzaya klasik bir örnek, standart topolojiyle donatılmış gerçek sayılar doğrusu \( \mathbb{R} \)’dir. Bu topolojide, her noktanın çevresinde bir aralık bulunduran kümeler açık küme kabul edilir. Bu yapı, süreklilik ve limit gibi kavramların topolojik açıdan incelenmesine olanak tanır.

Homeomorfizmler

Homeomorfizm, iki topolojik uzay arasında birebir, sürekli ve tersi de sürekli olan dönüşümdür. Bu dönüşüm temel topolojik özellikleri korur.

İki uzay arasında bir homeomorfizma varsa, topoloji açısından bu iki uzay özünde aynı kabul edilir.

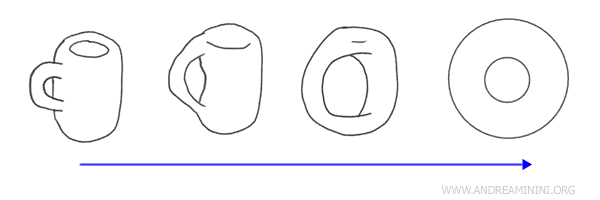
Örnek: Bir kahve fincanının sürekli dönüşümlerle simit şekline dönüştürülmesi, homeomorfizme klasik bir örnektir. Her iki nesne de tek bir deliğe sahiptir ve kesme ya da yapıştırma olmadan sürekli dönüşümlerle birbirine dönüştürülebilir. Böylece temel topolojik özellikler korunur.

Geometri ve Topoloji

Geometri ve topoloji farklı alanlar olsa da birbirleriyle yakından ilişkilidir; her biri matematiksel uzayların farklı yönlerini inceler.

• Geometri, mesafeler, açılar ve ölçülerle ilgili özelliklere odaklanır; somut şekiller ve bunların mekânsal ilişkilerini inceler. Örneğin, bir şeklin döndürülmesi mesafeleri koruyan geometrik bir dönüşümdür.
  

  En tanıdık geometri Öklid geometrisidir, fakat Öklid dışı geometriler, Öklid’in beşinci aksiyomunu (paralellik aksiyomu) esneterek ya da reddederek yeni ufuklar açar.

• Topoloji, yırtılma ya da yapıştırma olmaksızın yapılan sürekli dönüşümlerde değişmeden kalan özellikleri inceler. Nitel yönlere odaklanır: süreklilik, bağlantılar ve şekillerin esnek yapısı. Örneğin, bir küpün küreye dönüştürülmesi, noktalar arasındaki bağlantıları ve genel sürekliliği korur; bu tipik bir topolojik dönüşümdür.
  

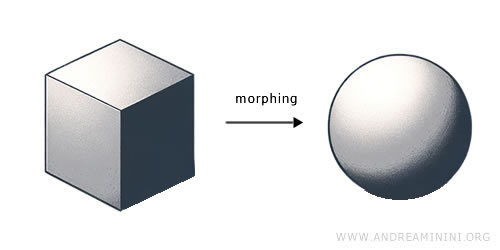
  Örnek: Kilden yapılmış bir küp, malzeme eklenmeden ya da çıkarılmadan sıkıştırılarak bir küreye dönüştürülebilir. Bu dönüşüm sürekliliği ve bağlantıları korur; homeomorfizmin klasik bir örneğidir.
  

Farklılıklarına rağmen topoloji ve geometri birbirine bağlıdır; topoloji çoğu zaman geometrinin genelleştirilmiş bir biçimi olarak görülür.

Topoloji, geometrinin daha katı çerçevesinin aksine, uzayların soyut özelliklerini incelemeye yönelir.

Topolojinin Dalları

Topoloji, matematik ve bilimin birçok alanında uygulanır; her dal topolojik uzayların farklı yönlerine odaklanır.

• Geometrik Topoloji: Bu dalda, yırtma ya da yapıştırma olmadan yapılan germe, sıkıştırma ve katlama gibi dönüşümlerde korunan özellikler incelenir. Süreklilik, bağlantı, kompaktlık ve sınırlar gibi kavramlar mesafeden bağımsız olarak ele alınır.
• Genel Topoloji (Nokta-Küme Topolojisi): Bu dal topolojik uzayları soyut biçimde inceler ve açık ve kapalı kümeler, süreklilik, kompaktlık, bağlantı, metrik uzaylar ve fonksiyon uzayları gibi kavramlara odaklanır.
• Cebirsel Topoloji: Cebirsel topoloji, cebirsel yöntemlerle topolojik uzayların incelenmesini sağlar ve bu uzayların özelliklerini daha iyi anlamak için cebirsel yapılarla bağ kurar.
• Diferansiyel Topoloji: Bu dal, diferansiyel hesap yöntemleriyle, özellikle yerel olarak Öklid uzayına benzeyen topolojik uzayların özelliklerini inceler. Böylece teğetlik ve türevlenebilirlik gibi kavramlar tanımlanabilir.
• Uygulamalı Topoloji: Uygulamalı topoloji, saf matematiğin dışında veri analizi, ağ bilimi, mühendislik ve hesaplamalı biyoloji gibi alanlarda topolojik yöntemlerin kullanımını kapsar.

Topolojinin her dalı, kendine özgü bakış açıları, yöntemleri ve uygulamalarıyla topolojik kavramların zenginliğini ve esnekliğini ortaya koyar.