Yolla bağlanabilir uzaylar
Bir topolojik uzay S, içindeki herhangi iki nokta A ve B’yi uzayın dışına çıkmadan birbirine bağlayan sürekli bir yol varsa yolla bağlanabilir olarak adlandırılır.
Kenarlarını hesaba katmadığımız bir kâğıt parçasını düşün.
Bu yüzey, kesintisiz bir alanı temsil eder ve sınırları dışarıda bıraktığı için açık bir uzay kabul edilir.
Böyle bir yüzeyde, A ve B gibi herhangi iki nokta arasında kalemi kâğıttan kaldırmadan bir çizgi çizebilirsin.
Kısacası, çizilen yol A ve B noktalarını kapsayan uzayın dışına çıkmaz.
Her yolla bağlanabilir uzay, zaten bağlı bir uzaydır.
Bu kulağa doğal gelebilir: çünkü eğer bir uzay bağlı değilse, ayrı parçalara ayrılmış demektir ve böyle bir durumda, iki noktanın sürekli bir yolla bağlanması uzayın dışına çıkmadan mümkün değildir.
Ancak tersi doğru olmak zorunda değildir. Her bağlı uzay mutlaka yolla bağlanabilir değildir.
İlk anda sezgiye ters gelse de, bu durum gerçekten gerçekleşebilir.
Örneğin, iki küme alalım: Q ve T
$$ Q = \{ \forall \ x \ \in R-\{ 0 \} \ , \ \sin( \frac{1}{x} ) \} $$
$$ T = \{ \ 0 \} $$
Q kümesi, sıfır hariç tüm reel sayılar için tanımlı olan $\sin(1/x)$ fonksiyonunun üzerindeki noktaları içerir. Ancak $x=0$ noktasında tanımsızdır, çünkü burada sıfıra bölme söz konusudur ve bu işlem tanımlanamaz.
T kümesi ise yalnızca $0$ noktasından oluşur.
Q ve T kümeleri, sürekli sin(1/x) fonksiyonunun grafiğinde görüldüğü gibi, sonsuz derecede yakın konumdadır.
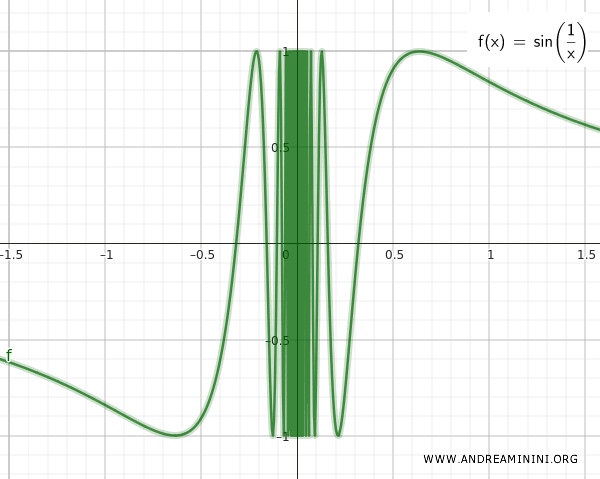
S kümesi, Q ve T’nin birleşimidir.
$$ S = Q \cup T $$
S kümesi bağlıdır, çünkü her $\epsilon > 0$ için, $0$ noktasının etrafındaki $(0-\epsilon,\; 0+\epsilon)$ aralığı Q kümesinden noktalar içerir.
Bunun nedeni, $0$ noktasının $\sin(1/x)$ fonksiyonunun bir yığılma noktası olmasıdır.
Yine de, S yolla bağlanabilir değildir, çünkü Q kümesindeki herhangi bir noktayı T kümesindeki sıfır noktasıyla birleştiren sürekli bir yol yoktur.
Not: Eğer fonksiyon $f(x)=1/x$ olsaydı, durum farklı olurdu. Bu durumda Q ve T kümeleri açıkça ayrıktır, yani birbirine sonsuz derecede yakın değildir.
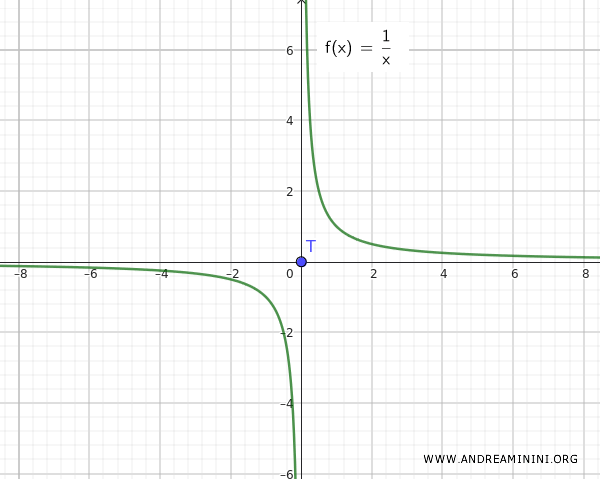
Bu örnek, Q={∀ x ∈ R-{0}, 1/x} kümesiyle tek başına T={0} noktasının birleşiminin, bu nokta (örneğin $0$) aynı zamanda bir yığılma noktası değilse, mutlaka bağlı bir küme oluşturmayacağını gösterir.
Ve benzeri durumlar da vardır.