Topolojide açık kümeler

Bir A kümesi, eğer A’daki her bir eleman x için (x∈A) tamamen A’nın içinde kalan bir komşuluk (mahalle) bulunabiliyorsa, açık küme olarak adlandırılır.

 

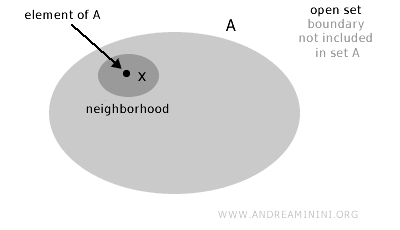
Başka bir deyişle, bir kümenin sınır noktaları o kümeye ait değilse, o küme açık kabul edilir.

Daha biçimsel olarak söylemek gerekirse, topolojik bir uzay X’in alt kümesi olan A, eğer A’daki her nokta x için x’in tamamen A içinde kalan bir komşuluğu varsa, açıktır.

Not. Bu tanım, kümedeki her noktanın çevresinde, dış sınıra değmeden tamamen küme içinde yer alan bir “bölge” bulunabileceğini ifade eder.

Basit bir örnek

Bir doğru üzerindeki açık kümeye en basit örnek, açık aralıktır.

Açık aralık nedir? \( \mathbb{R} \) üzerinde bir açık aralık, \( a < x < b \) koşulunu sağlayan tüm gerçek sayılardan oluşan kümedir. Burada \( a \) ve \( b \), \( a < b \) olacak şekilde seçilmiş iki gerçek sayıdır.

Bu aralık (a,b) biçiminde gösterilir; parantezler, uç noktalar a ve b’nin kümeye dahil edilmediğini belirtir.

Örneğin, (3,10) aralığı, gerçek sayı doğrusunda açık bir kümedir.

Bu durumda A kümesi, 3 ile 10 arasındaki uç noktalar hariç sonsuz sayıda sayıdan oluşur.

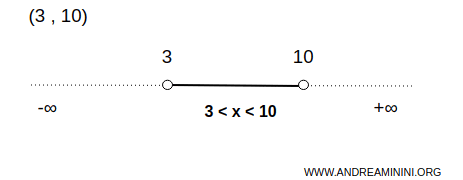
Bu, aralık içindeki her nokta x için, x’in çevresinde tamamen (3,10) içinde kalan küçük bir açık aralık seçilebileceği anlamına gelir.

Örneğin x=3.1 için (3.09,3.11) aralığını alırsak, bu aralık tamamen (3,10) kümesinin içindedir.

Aynı durum (3,10) aralığındaki tüm diğer noktalar için de geçerlidir; çünkü herhangi iki gerçek sayı arasında sonsuz sayıda başka gerçek sayı bulunur.

Not. (3,10) aralığı içindeki çok küçük bir sayı, örneğin 3.001 bile seçilse, 3.001±0.00000001 biçiminde bir komşuluk oluşturulabilir ve bu komşuluk açık aralık (3,10) içinde sonsuz sayıda gerçek sayı içerir.

Bu, açık küme kavramının tek boyutlu en sade örneğidir.

Diğer örnekler

Aynı kavram iki boyutlu uzaya - örneğin düzleme - de genişletilebilir.

Örneğin, merkezi orijinde (0;0) ve yarıçapı r=1 olan bir dairenin noktalar kümesini düşünelim:

$$ x^2+y^2<1 $$

Bu eşitsizlik, merkezden (0,0) uzaklığı 1’den küçük olan tüm noktaları tanımlar. Dolayısıyla, çevre üzerindeki noktalar dahil değildir; yalnızca dairenin içi bu kümeye aittir.

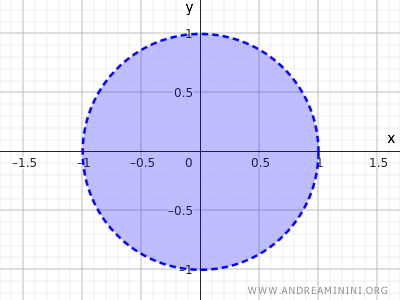
Bu da açık küme kavramına iki boyutlu bir örnektir.

Peki bir küme ne zaman kapalı olur?

Kapalı bir küme elde etmek için, yalnızca dairenin çevresindeki noktaları da kümeye dahil etmek yeterlidir:

$$ x^2+y^2 \le 1 $$

Bu durumda, kümedeki her noktanın tamamen küme içinde kalan bir komşuluğu olması koşulu artık sağlanmaz.

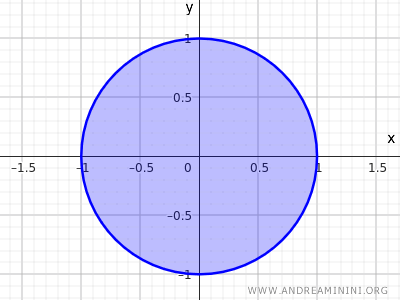
Kapalı küme durumunda, çevre üzerindeki noktaların tamamen küme içinde kalan bir komşuluğu yoktur.

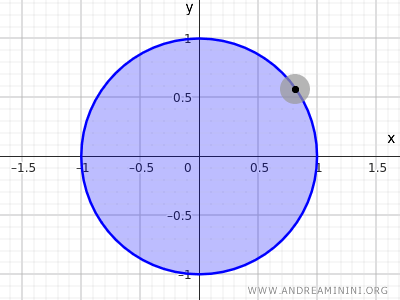
Not. Topolojide, $ x^2+y^2=1 $ denklemiyle tanımlanan daire, yalnızca çevre üzerindeki noktaları içerdiğinden ℝ² uzayında ne açık ne de kapalı bir kümedir. Buna karşılık, $ x^2+y^2<1 $ eşitsizliğiyle tanımlanan küme - yani iç noktaları içeren, fakat çevreyi içermeyen küme - açık kümedir. Çevre noktalarını da dahil eden $ x^2+y^2\le 1 $ kümesi ise bir kapalı küme oluşturur.

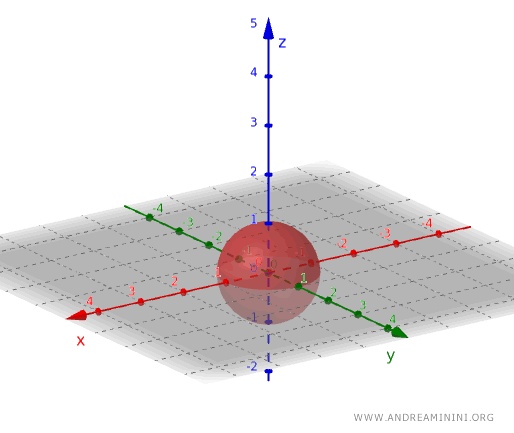
Aynı prensip üç boyutlu uzaya da uygulanabilir: Örneğin, bir kürenin yüzeyindeki noktalar hariç, yalnızca iç kısmındaki noktaları içeren küme açık bir küme oluşturur.

Bir topoloji seçmek

Açık aralıklar sezgisel olmaları sayesinde açık küme kavramını anlamak için oldukça yararlıdır.

Ancak açık küme kavramı, yalnızca açık aralıklarla sınırlı olmayan, çok daha soyut bir yapıya sahiptir.

Bu yüzden, temel fikri kavradıktan sonra konuyu daha derinlemesine incelemek gerekir.

Bir “açık küme”nin tanımı, bir uzaya uygulanan topolojiye bağlıdır.

Burada anlaşılması gereken en önemli nokta, açık küme tanımının seçilen topolojiye göre tamamen değişebileceğidir.

Yani herhangi bir küme, tanımlanan topolojiye bağlı olarak açık sayılabilir.

Topoloji nedir? Bir uzay üzerindeki topoloji, belirli kuralları sağlayan “açık” kabul edilen kümelerin bir ailesidir. Örneğin, açık kümelerin keyfi birleşimleri yine açık kümedir; sonlu sayıda açık kümenin kesişimi de yine açıktır.

Bu nedenle, açık kümeleri yalnızca en tanıdık örneklerle - açık aralıklar veya açık disklerle - sınırlamamak gerekir.

Topolojide “açık küme” kavramı çok daha kapsamlıdır ve ilk bakışta açık görünmeyen kümeleri de içerebilir.

Uygulamalı bir örnek

Yalnızca iki eleman içeren \( \{a, b\} \) uzayını düşünelim.

Bu uzayda en az iki farklı topoloji tanımlanabilir: trivial (önemsiz) topoloji ve ayrık topoloji.

• Trivial topoloji
  \( \{a, b\} \) üzerinde trivial topolojide yalnızca boş küme \( \emptyset \) ve tüm uzay \( \{a, b\} \) açık kümelerdir. Bu, en sade topolojidir ve boş küme ile tüm uzay dışında başka “açık yapı” içermez.
• Ayrık topoloji
  Ayrık topolojide \( \{a, b\} \)’nin her altkümesi açıktır. Dolayısıyla \( \{a\} \), \( \{b\} \), \( \{a, b\} \) ve \( \emptyset \) kümelerinin tümü açık kümelerdir. Ayrık topoloji, açık kümeler bakımından en zengin topolojidir; çünkü her nokta kombinasyonu bir açık küme oluşturur.

Şimdi \( \{a\} \) kümesini her iki topolojide de inceleyelim:

• Trivial topolojide {a} kümesi açık değildir.
  Bu topolojide, boş küme dışında eleman içeren tek açık küme \( \{a, b\} \)’dir.
• Ayrık topolojide {a} kümesi açıktır.
  Bu topolojide, \( \{a, b\} \)’nin her altkümesi - \( \{a\} \) ve \( \{b\} \) dahil - tanım gereği açıktır.

Dolayısıyla \( \{a\} \) kümesi, ayrık topoloji altında açıkken, trivial topoloji altında açık değildir.

Bu basit örnek, açık küme kavramının seçilen topolojiyle ne kadar yakından ilişkili olduğunu açıkça gösterir.

Açık küme teoremi

Teorem 1

Açık bir küme X ve bir topoloji T birlikte verildiğinde, bu ikili (X,T) bir topolojik uzay oluşturur. X’in bir alt kümesi olan S⊂X, eğer her bir eleman (ya da nokta) s∈S için tamamen S’nin içinde kalan bir komşuluk U varsa, yani U⊂S koşulu sağlanıyorsa, (X,T) topolojik uzayında açık bir kümedir.

Tanım gereği S, topolojik uzayın bir parçası olduğundan açık bir küme olarak kabul edilir.

Dolayısıyla S alt kümesi, içindeki her bir noktanın s∈S komşuluğu olarak düşünülebilir.

Bu durumda, her s∈S noktası için tanımlanan U_s komşuluğu, S’nin içinde yer alan açık bir kümedir.

$$ x \in U_s \subset S \subset X $$

Başka bir deyişle, bir açık küme, noktalarının açık komşuluklarının birleşimi olarak ifade edilebilir.

Dolayısıyla eğer bir alt küme S’deki her nokta s∈S için tamamen S içinde kalan bir komşuluk U_s bulunabiliyorsa, bu durumda S kümesi açık kabul edilir; çünkü S, açık kümelerin birleşiminden oluşur.

Özetle, bir küme, ancak ve ancak içindeki her nokta için tamamen küme içinde yer alan bir komşuluk varsa, açık kümedir.

Örnek. Üzerinde cam bilyeler bulunan bir masa hayal edin. Her bilye, belirli bir kümenin bir noktasını temsil etsin. Bu kümenin “açık” olduğunu söylemek, her bilyenin çevresinde, masanın kenarına değmeden hareket edebileceği kadar boşluk bulunduğunu belirtmekle aynıdır. Eğer her bilyenin çevresine, masanın kenarlarına temas etmeden tamamen masa üzerinde kalan bir daire çizebiliyorsam, bu bilyeler kümesi bir “açık küme”yi temsil eder. Başka bir ifadeyle, kümenin açıklığı, hangi bilyeyi seçersem seçeyim, etrafında hâlâ kümenin içinde kalan bir “boşluk” bulunduğu anlamına gelir.

Teorem 2

Bir \( X \) kümesi ve onun üzerinde tanımlanmış bir topolojinin tabanı \( B \) verilsin. \( A \subset X \) alt kümesi, ancak ve ancak her \( x \in A \) noktası için \( B \)’de yer alan bir taban elemanı \( B_x \) mevcutsa, yani \( x \in B_x \) ve \( B_x \subseteq A \) koşulu sağlanıyorsa, \( B \) tarafından oluşturulan topolojide açık bir kümedir.

Bu teorem, bir taban tarafından tanımlanan topolojilerin temel özelliğini açıkça ortaya koyar.

Basitçe ifade etmek gerekirse, açık bir \( A \) kümesindeki her noktanın çevresinde, tabana ait ve tamamen \( A \)’nın içinde kalan bir komşuluk \( B_x \) bulunmalıdır.

Bu durum, \( A \) kümesinin gerçekten de \( B \) tabanı tarafından oluşturulan topolojide açık olduğunu doğrular.

İspat. Eğer A, X kümesi üzerinde B tabanı tarafından oluşturulan topolojide açık bir küme ise, tanım gereği A, taban elemanlarının birleşimidir. Dolayısıyla A’daki her x noktası en az bir taban elemanı \( B_x \)’ye aittir ve bu \( B_x \) tamamen A’nın içindedir. Yani \( B_x \subseteq A \). Bu akıl yürütmenin tersi de geçerlidir: A’daki her x noktası için tamamen A’nın içinde yer alan en az bir taban elemanı \( B_x \) mevcutsa, bu durumda A, B tarafından oluşturulan topolojide açık bir kümedir.

Örnek

\( X = \{1, 2, 3, 4, 5\} \) kümesini ve \( X \) üzerinde tanımlı bir topolojinin tabanı olarak \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \) kümesini ele alalım. Şimdi \( A = \{1, 2, 3\} \) kümesinin açık olup olmadığını inceleyelim.

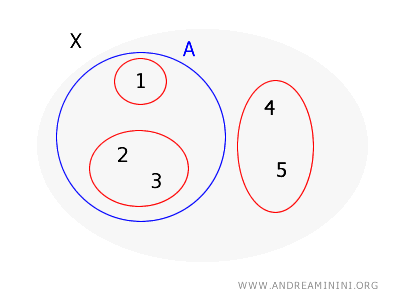
\( A \)’daki her nokta için onu içeren ve tamamen \( A \)’nın içinde kalan bir taban kümesi bulmam gerekir:

• \( 1 \) noktası için, \( 1 \)’i içeren ve tamamen \( A \)’da yer alan taban kümesi \( \{1\} \)’dir.
• \( 2 \) noktası için, \( \{2, 3\} \) taban kümesi \( 2 \)’yi içerir ve tamamen \( A \)’nın içindedir.
• \( 3 \) noktası için, aynı \( \{2, 3\} \) taban kümesi \( 3 \)’ü içerir ve tamamen \( A \)’nın içindedir.

\( A \)’daki her nokta, tamamen \( A \)’nın içinde yer alan bir taban kümesiyle örtüldüğünden teoremin koşulu sağlanmıştır.

Dolayısıyla, \( A \) kümesi \( B \) tabanı tarafından oluşturulan topolojide açık bir kümedir.

Örnek 2

Aynı \( X = \{1, 2, 3, 4, 5\} \) kümesini ve \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \) tabanını tekrar ele alalım.

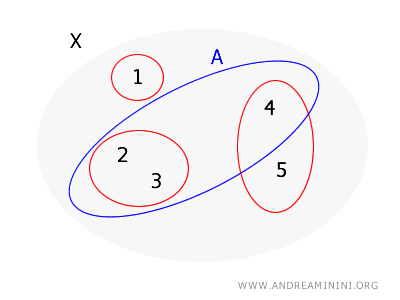
Bu kez \( A = \{2, 3, 4\} \) kümesinin açık olup olmadığını inceleyelim.

• \( 2 \) noktası için \( \{2, 3\} \) taban kümesi tamamen \( A \)’nın içindedir.
• \( 3 \) noktası için de aynı \( \{2, 3\} \) taban kümesi geçerlidir ve bu küme \( 3 \)’ü içerir, ayrıca tamamen \( A \)’nın içindedir.
• \( 4 \) noktası içinse, onu içeren ve tamamen \( A \)’da kalan bir taban kümesi yoktur; çünkü 4’ü içeren tek taban kümesi \( \{4, 5\} \)’tir ve bu küme 5’i de kapsadığı için \( A \)’nın içinde değildir.

Dolayısıyla teoreme göre, \( A \) kümesi \( B \) tabanı tarafından oluşturulan topolojide açık bir küme değildir; çünkü \( A \)’daki tüm noktalar için tamamen \( A \)’nın içinde kalan bir taban kümesi bulunmamaktadır.

Tamamlayıcı notlar

Açık kümeler hakkında bazı genel gözlemler ve önemli hatırlatmalar:

• Bir A kümesi ancak ve ancak A = Int(A) eşitliği sağlanıyorsa açıktır
  Bir topolojik uzay \( X \)’teki bir \( A \) kümesi, yalnızca kendi iç kısmıyla çakıştığında açıktır. Bir kümenin iç kısmı, Int(A) ile gösterilir ve \( A \) içinde yer alan tüm açık kümelerin birleşimi olarak tanımlanır: $$ A = \text{Int}(A) $$

Bu gözlem, açık kümelerin doğasını anlamak için temel bir bağlantı kurar.

Benzer ilkeler diğer topolojik kavramlar için de geçerlidir.