Açık Dikdörtgenlerle Tanımlanan Topoloji

Açık dikdörtgenlerle tanımlanan topoloji, R² düzleminde açık kümelerin açık dikdörtgenlerin birleşimiyle tanımlandığı temel bir topolojik yapıdır. Her dikdörtgen, Kartezyen eksenler üzerindeki iki açık aralığın çarpımıyla elde edilir. Bu yapı, iki boyutlu uzayda noktalar arasındaki ilişkileri anlamak için güçlü bir başlangıç noktası sunar.

Bu topolojide tüm yapı, açık dikdörtgen komşuluklardan oluşan bir taban üzerine kuruludur. Başka bir ifadeyle, bu dikdörtgenler düzlemdeki açık kümelerin temelini oluşturur.

Bir $ U \subseteq \mathbb{R}^2 $ kümesinin açık olabilmesi için, içerdiği her $ (x, y) $ noktası etrafında hem bu noktayı kapsayan hem de tamamen $ U $’nun içinde kalan bir açık dikdörtgen bulunması gerekir.

Bu nedenle açık dikdörtgenler, Öklid düzleminin topolojisini tanımlayan temel yapı taşlarıdır.

$$ B = \{ (a, b) \times (c, d) \,|\, a

Burada $ a, b, c, d $ gerçek sayılardır ve $ a < b $, $ c < d $ koşulları bu dikdörtgenlerin sınırlarını belirler. Böylece bu dikdörtgenler, $ \mathbb{R}^2 $ düzlemi üzerinde bir topoloji tabanı oluşturur.

Bu yaklaşım, genellikle açık disklerle tanımlanan standart topolojiye farklı bir alternatif sunar. Aynı topolojik yapıyı, bu kez daireler yerine dikdörtgenlerle açıklamış oluruz.

Not: Bu durum, topolojik yapının biçimden bağımsız olduğunu gösterir. Daireler ya da dikdörtgenler gibi farklı şekiller, açık kümelerin genel tanımını değiştirmeden bir taban oluşturabilir. Şekil değişse bile, bu kümelerin birleşimi $ \mathbb{R}^2 $’nin topolojisi için tutarlı bir yapı meydana getirir.

Bir Açık Dikdörtgenin Görselleştirilmesi

$ \mathbb{R}^2 $ düzleminde bir açık dikdörtgen, her eksen boyunca tanımlanan iki açık aralığın Kartezyen çarpımıyla elde edilir.

Örneğin, $ x $-ekseni boyunca $ (1, 3) $ ve $ y $-ekseni boyunca $ (2, 4) $ açık aralıklarını alalım.

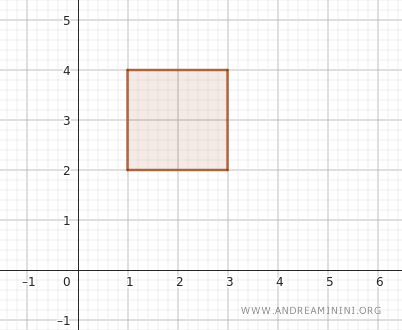
açık bir dikdörtgen örneği

Bu aralıklardan oluşan açık dikdörtgen, $ x $’in 1 ile 3 arasında, $ y $’nin ise 2 ile 4 arasında olduğu tüm $ (x, y) $ noktalarından meydana gelir.

Biçimsel olarak bu dikdörtgen $ (1, 3) \times (2, 4) $ şeklinde gösterilir.

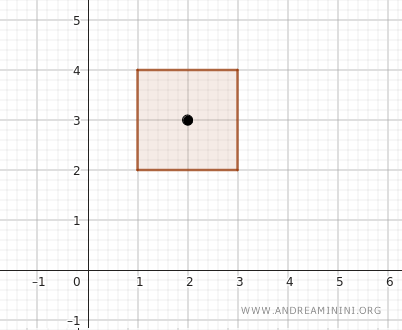
(2,3) noktası

Bu bölgeden bir nokta seçelim, örneğin $ (2, 3) $. Bu noktada $ x $ koordinatı 1’den büyük, 3’ten küçük; $ y $ koordinatı ise 2’den büyük, 4’ten küçüktür. Yani nokta açık dikdörtgenin içindedir.

Not: Dikdörtgenin kenarları bu kümenin bir parçası değildir. Dolayısıyla $ (1, y) $, $ (3, y) $, $ (x, 2) $ ve $ (x, 4) $ gibi noktalar açık dikdörtgenin dışında kalır.