Bir Kümenin Sınırı

Bir $ x $ noktası, $ A $ kümesinin sınırına aittir; eğer $ x $ noktasının her komşuluğu hem $ A $ kümesiyle hem de $ A $ kümesinin tümleyeniyle, yani $ X - A $ ile kesişiyorsa.

Daha sezgisel bir ifadeyle, $ x $ noktasının ne tamamen $ A $ içinde ne de tamamen $ A $ dışında kalan bir komşuluğunu bulamıyorsak, bu nokta $ A $ kümesinin sınırında yer alır.

Somut Bir Örnek
İspat

Somut Bir Örnek

Kavramı daha net görmek için basit ama öğretici bir örnek üzerinden ilerleyelim.

Gerçek sayılar doğrusu $ \mathbb{R} $ üzerinde tanımlı olan

$ A = (0, 1) $

kümesini ele alalım.

Bu kümede 0 ve 1 noktaları özel bir role sahiptir. Çünkü bu noktalardan herhangi birinin etrafında aldığımız her komşuluk, kaçınılmaz olarak hem $ (0,1) $ aralığının bir kısmını hem de bu aralığın dışındaki bir kısmı içerir.

1 Noktası
Sonsuz derecede küçük ε için seçilen her $ (1-\epsilon, 1+\epsilon) $ komşuluğu, $ (1-\epsilon,1) $ kısmıyla $ (0,1) $ kümesi içinde yer alır. Buna karşılık $ (1,1+\epsilon) $ kısmı kümenin dışındadır. Bu durum, 1 noktasının $ A $ kümesinin sınırında bulunduğunu açıkça gösterir.
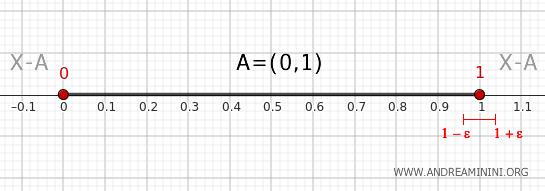
0 Noktası
Aynı mantık 0 noktası için de geçerlidir. Yeterince küçük ε ile tanımlanan her $ (0-\epsilon, 0+\epsilon) $ komşuluğu, $ (0,0+\epsilon) $ parçasıyla $ (0,1) $ içinde kalır; $ (0-\epsilon,0) $ parçasıyla ise bu aralığın dışına taşar. Dolayısıyla 0 noktası da bir sınır noktasıdır.
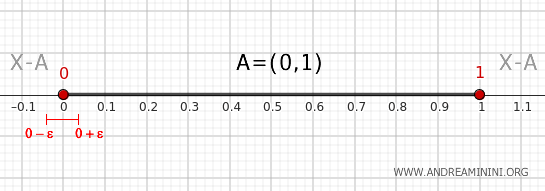
(0,1) aralığının içindeki bir nokta
Aralığın içinde bulunan herhangi bir $ x $ noktası için, yeterince küçük ε seçildiğinde $ (x-\epsilon, x+\epsilon) $ komşuluğu bütünüyle $ (0,1) $ içinde kalır ve $ X-A $ ile kesişmez. Bu nedenle bu tür noktalar sınır noktası değildir.
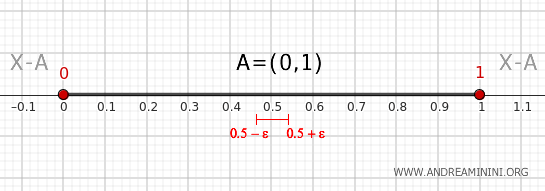
(0,1) aralığının dışındaki bir nokta
0 ve 1 dışında kalan, $ (0,1) $ aralığının dışındaki herhangi bir nokta için ise durum tersinedir. Yeterince küçük ε ile alınan $ (x-\epsilon, x+\epsilon) $ komşuluğu tamamen $ X-A $ içinde yer alır ve $ (0,1) $ ile kesişmez. Bu nedenle $ [0,1] $ aralığının dışındaki noktalar da sınır noktası değildir.

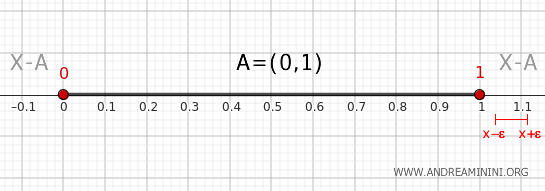
Bu gözlemlerden şu sonuca ulaşırız: $ A $ kümesinin sınırı yalnızca uç noktalarından oluşur.

$$ \partial A = \{0,1\} $$

Kısaca özetlemek gerekirse, bir noktayı sınır noktası yapan şey, onun etrafında ne bütünüyle kümenin içinde ne de bütünüyle kümenin dışında kalan bir komşuluk bulunamamasıdır.

İspat

Bu tanımı doğrulamak için iki yönlü bir akıl yürütme yapalım.

1] $ x $ noktası, $ A $ kümesinin bir sınır noktasıdır

$ A $ kümesinin sınırında bulunan bir $ x $ noktası ele alalım:

$$ x \in \partial A $$

Tanım gereği bu ifade, $ x \in \text{Cl}(A) $ ve aynı zamanda $ x \notin \text{Int}(A) $ koşullarının birlikte sağlandığını belirtir.

$ x \in \text{Cl}(A) $ olması, $ x $ noktasının her komşuluğunun $ A $ kümesiyle kesiştiği anlamına gelir.

Öte yandan $ x \notin \text{Int}(A) $ olduğu için, hiçbir komşuluk bütünüyle $ A $ içinde kalamaz. Bu da her komşuluğun zorunlu olarak $ X-A $ ile kesişmesini gerektirir.

Dolayısıyla $ x $ noktasının her komşuluğu hem $ A $ hem de $ X-A $ ile kesişir.

2] $ x $ noktasının her komşuluğu hem $ A $ hem de $ X-A $ ile kesişir

Şimdi ters yönden düşünelim ve $ x $ noktasının her komşuluğunun hem $ A $ hem de $ X-A $ ile kesiştiğini varsayalım.

Bu durumda $ x \in \text{Cl}(A) $ ve $ x \in \text{Cl}(X-A) $ elde edilir.

$ \text{Cl}(X-A) = X - \text{Int}(A) $ eşitliği kullanıldığında, buradan doğrudan $ x \notin \text{Int}(A) $ sonucu çıkar.

Sonuç olarak $ x \in \text{Cl}(A) $ ve $ x \notin \text{Int}(A) $ olur; yani

$$ x \in \text{Cl}(A) - \text{Int}(A) = \partial A $$

Bu da $ x $ noktasının gerçekten $ A $ kümesinin bir sınır noktası olduğunu kesin biçimde ortaya koyar.