Teorema Karakterisasi Batas Himpunan

Suatu titik $ x $ dikatakan berada pada batas sebuah himpunan $ A $ apabila setiap lingkungan di sekitar $ x $ selalu beririsan, baik dengan himpunan $ A $ maupun dengan komplemennya, yaitu $ X - A $.

Intinya sederhana. Jika tidak ada satu pun lingkungan dari $ x $ yang sepenuhnya berada di dalam $ A $ atau sepenuhnya berada di luar $ A $, maka titik tersebut berada pada batas himpunan $ A $.

Contoh Praktis
Pembuktian

Contoh Praktis

Agar konsep ini lebih mudah dipahami, mari kita lihat contoh yang konkret dan familiar.

Ambil himpunan $ A = (0, 1) $ pada garis bilangan real $ \mathbb{R} $.

Titik 0 dan 1 merupakan titik batas dari $ A $. Alasannya, setiap lingkungan di sekitar 0 atau 1 selalu mencakup sebagian titik di dalam interval $ (0, 1) $ dan sebagian titik di luar interval tersebut.

Titik 1
Setiap lingkungan $ (1-\epsilon, 1+\epsilon) $ dengan ε yang sangat kecil selalu mengandung bagian $ (1-\epsilon,1) $ yang berada di dalam $ (0,1) $, serta bagian $ (1,1+\epsilon) $ yang berada di luar $ (0,1) $. Karena itu, titik 1 termasuk titik batas dari himpunan $ A $.
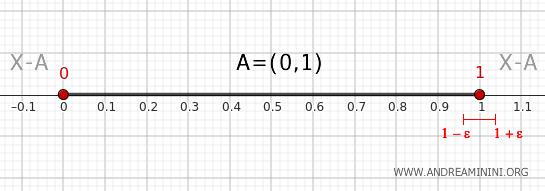
Titik 0
Dengan alasan yang sama, setiap lingkungan $ (0-\epsilon, 0+\epsilon) $ dengan ε yang sangat kecil selalu memiliki bagian $ (0,0+\epsilon) $ di dalam $ (0,1) $ dan bagian $ (0-\epsilon,0) $ di luar $ (0,1) $. Maka, titik 0 juga merupakan titik batas dari $ A $.
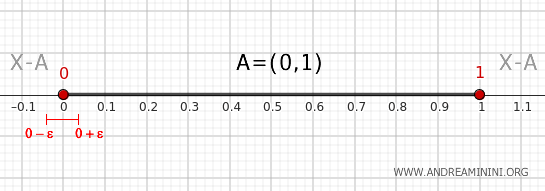
Titik di dalam interval (0,1)
Untuk setiap titik $ x $ di dalam interval $ (0,1) $, selalu dapat ditemukan lingkungan $ (x-\epsilon, x+\epsilon) $ dengan ε yang sangat kecil dan sepenuhnya berada di dalam $ A $. Lingkungan ini tidak beririsan dengan $ X - A $. Oleh sebab itu, titik-titik interior dari interval $ (0,1) $ bukanlah titik batas.
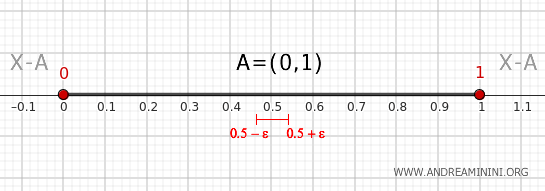
Titik di luar interval (0,1)
Setiap titik di luar interval $ (0,1) $, kecuali 0 dan 1, memiliki lingkungan $ (x-\epsilon, x+\epsilon) $ dengan ε yang sepenuhnya berada di dalam $ X - A $ dan tidak beririsan dengan $ A $. Dengan demikian, titik-titik di luar interval tertutup $ [0,1] $ bukan merupakan titik batas dari $ A $.

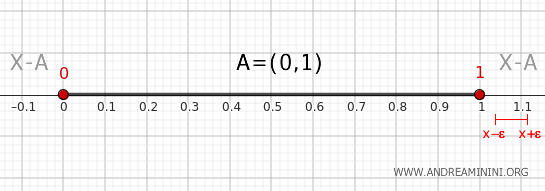
Dari pembahasan ini dapat disimpulkan bahwa satu-satunya titik batas dari himpunan $ A = (0,1) $ adalah 0 dan 1.

$$ \partial A = \{0,1\} $$

Secara umum, sebuah titik $ x $ berada pada batas himpunan $ A $ apabila setiap lingkungan di sekitar $ x $ selalu memotong $ A $ dan juga memotong bagian luarnya.

Pembuktian

Pembuktian berikut menunjukkan bahwa definisi batas di atas bersifat ekuivalen dari dua arah.

1] Jika $ x $ adalah titik batas dari $ A $

Misalkan suatu titik $ x $ berada pada batas himpunan $ A $.

$$ x \in \partial A $$

Berdasarkan definisi, hal ini berarti bahwa $ x \in \text{Cl}(A) $ dan $ x \notin \text{Int}(A) $.

Keanggotaan $ x \in \text{Cl}(A) $ menjamin bahwa setiap lingkungan dari $ x $ beririsan dengan $ A $.

Sementara itu, karena $ x \notin \text{Int}(A) $, tidak ada lingkungan dari $ x $ yang sepenuhnya berada di dalam $ A $. Akibatnya, setiap lingkungan tersebut harus beririsan dengan $ X - A $.

Dengan demikian, setiap lingkungan dari $ x $ selalu beririsan dengan $ A $ dan juga dengan $ X - A $.

2] Jika setiap lingkungan dari $ x $ beririsan dengan $ A $ dan $ X - A $

Sekarang, andaikan setiap lingkungan dari titik $ x $ selalu beririsan dengan $ A $ dan juga dengan $ X - A $.

Dari kondisi ini dapat disimpulkan bahwa $ x \in \text{Cl}(A) $ serta $ x \in \text{Cl}(X - A) $.

Karena berlaku hubungan $ \text{Cl}(X - A) = X - \text{Int}(A) $, maka diperoleh bahwa $ x \notin \text{Int}(A) $.

Oleh karena itu, $ x \in \text{Cl}(A) $ dan $ x \notin \text{Int}(A) $, sehingga dapat disimpulkan bahwa $ x \in \partial A $.

Ini menunjukkan bahwa titik $ x $ memang merupakan titik batas dari himpunan $ A $.