Himpunan A Tertutup Jika dan Hanya Jika Batasnya Merupakan Subhimpunan dari A

Dalam topologi, batas $ \partial A $ dari suatu himpunan $ A $ merupakan subhimpunan dari $ A $ jika dan hanya jika $ A $ adalah himpunan tertutup. \[ \partial A \subseteq A \Leftrightarrow A \text{ tertutup} \]

Contoh Praktis
Pembuktian

Contoh Praktis

Contoh 1

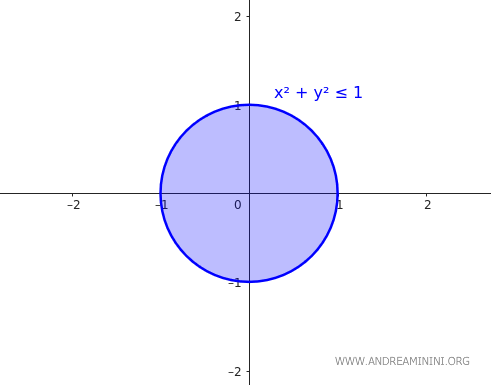
Misalkan $ A $ adalah lingkaran tertutup dengan jari-jari 1 yang berpusat di titik asal pada ruang Euklides $\mathbb{R}^2$.

$$ A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 1 $$

Pada contoh ini, batas dari $ A $ adalah keliling lingkaran dengan jari-jari 1:

$$ \partial A = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 = 1 $$

Karena $ A $ merupakan lingkaran tertutup, semua titik pada keliling lingkaran tersebut termasuk ke dalam himpunan $ A $. Dengan kata lain, batasnya sepenuhnya termuat di dalam $ A $:

$$ \partial A \subseteq A $$

Hal ini menunjukkan bahwa $ A $ memang merupakan himpunan tertutup.

contoh lingkaran tertutup yang memuat seluruh titik batasnya

Contoh 2

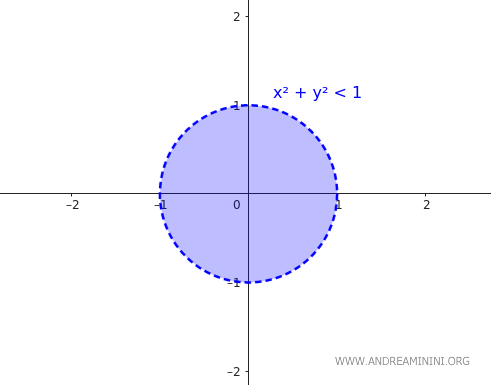
Sebagai pembanding, perhatikan himpunan $ B $ yang merupakan lingkaran terbuka dengan jari-jari 1 dan pusat di titik asal.

$$ B = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 < 1 $$

Batas dari $ B $ tetap sama, yaitu keliling lingkaran dengan jari-jari 1:

$$ \partial B = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 = 1 $$

Namun, karena $ B $ adalah lingkaran terbuka, titik-titik pada keliling lingkaran tidak termasuk di dalam himpunan tersebut. Akibatnya:

$$ \partial B \nsubseteq B $$

Dari sini terlihat bahwa $ B $ bukanlah himpunan tertutup.

contoh lingkaran terbuka yang tidak memuat titik-titik batasnya

Kedua contoh ini memberikan gambaran yang jelas: himpunan tertutup selalu memuat batasnya sendiri, sedangkan himpunan terbuka tidak.

Pembuktian

Untuk memahami pernyataan ini secara umum, kita membaginya ke dalam dua arah pembuktian.

1] Jika Batas dari A Merupakan Subhimpunan dari A, maka A Tertutup

Andaikan $ \partial A \subseteq A $, artinya semua titik batas dari himpunan $ A $ berada di dalam $ A $.

Tujuan kita adalah menunjukkan bahwa $ A $ merupakan himpunan tertutup.

Secara definisi, batas dari $ A $ diberikan oleh $ \partial A = \overline{A} \cap \overline{A^c} $, dengan $ \overline{A} $ menyatakan penutupan dari $ A $ dan $ \overline{A^c} $ penutupan dari komplemen $ A $.

Setiap titik pada batas $ \partial A $ adalah titik akumulasi dari $ A $ atau dari komplemennya. Jika semua titik tersebut berada di dalam $ A $, maka $ A $ memuat seluruh titik akumulasinya.

Menurut definisi topologi, suatu himpunan yang memuat semua titik akumulasinya adalah himpunan tertutup. Dengan demikian, $ A $ harus tertutup.

2] Jika A Tertutup, maka Batasnya Merupakan Subhimpunan dari A

Sekarang andaikan bahwa $ A $ adalah himpunan tertutup. Kita akan menunjukkan bahwa batasnya termuat di dalam $ A $.

Karena $ A $ tertutup, maka himpunan ini sama dengan penutupannya:

$$ A = \text{Cl}(A) $$

Batas dari $ A $ didefinisikan sebagai irisan antara penutupan dari $ A $ dan penutupan dari komplemennya:

$$ \partial A = \text{Cl}(A) \cap \text{Cl}(A^c) $$

Dengan menggantikan $ \text{Cl}(A) $ oleh $ A $, diperoleh:

$$ \partial A = A \cap \text{Cl}(A^c) $$

Rumus ini menunjukkan bahwa setiap titik pada batas $ A $ merupakan elemen dari $ A $. Oleh karena itu, batas $ \partial A $ adalah subhimpunan dari $ A $.

3] Kesimpulan

Kesimpulannya, sebuah himpunan $ A $ tertutup jika dan hanya jika batasnya $ \partial A $ merupakan subhimpunan dari $ A $. Pernyataan ini memberikan karakterisasi yang sederhana dan intuitif mengenai himpunan tertutup dalam topologi.

Dan seterusnya.