İki Kümenin İçlerinin Birleşimi Nedir?

İki küme $ A $ ve $ B $’nin içlerinin birleşimi, her zaman bu iki kümenin birleşiminin iç kümesinin bir altkümesidir. \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] Ancak bu iki kümenin içleri genellikle eşit değildir.

Bu özellik, topolojide oldukça temel bir kavramı açıklar: iki kümenin içlerini birleştirdiğimizde, bu birleşim her zaman kümelerin birleşiminin iç kısmının içinde yer alır. Fakat bu, her zaman tam bir eşitlik anlamına gelmez.

Kavramı Basitçe Anlamak

İç küme (ya da bir kümenin “içi”), o kümenin sınırına dokunmadan tamamen içinde kalan noktaların tümüdür. Başka bir deyişle, bir noktanın etrafında küçük bir alan çizebiliyorsak ve bu alan tamamen kümenin içinde kalıyorsa, o nokta iç noktadır.

İşte bu nedenle, “içlerin birleşimi” ile “birleşimin içi” aynı şey değildir. Şimdi bunu örneklerle adım adım görelim.

1. Örnek: Kesişen Açık Aralıklar

\(\mathbb{R}\) üzerindeki iki açık aralığı düşünelim:

$$ A = (0, 2) \quad \text{ve} \quad B = (1, 3) $$

Açık aralıkların içi kendileridir:

$$ \text{Int}(A) = (0, 2) \quad \text{ve} \quad \text{Int}(B) = (1, 3) $$

Bu iki aralığın içlerinin birleşimi şöyle olur:

$$ (0, 2) \cup (1, 3) = (0, 3) $$

Aralıklar birbirini kesiştirdiği için, birleşimleri de $(0, 3)$ aralığına denk gelir. Dolayısıyla:

$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) = (0, 3) $$

Bu durumda eşitlik geçerlidir.

2. Örnek: Kapanış Noktalarıyla Fark Yaratan Durum

Şimdi kapalı aralıkları ele alalım:

$$ A = [0, 2] \quad \text{ve} \quad B = [2, 3] $$

Kapalı aralıkların içleri, uç noktalar hariçtir:

$$ \text{Int}(A) = (0, 2) \quad \text{ve} \quad \text{Int}(B) = (2, 3) $$

Birleşimin içi ise:

$$ \text{Int}(A \cup B) = (0, 3) $$

Burada dikkat edilmesi gereken nokta şudur: $2$ noktası, birleşimin içindedir fakat ne $A$’nın ne de $B$’nin içindedir.

Bu nedenle:

$$ 2 \in \text{Int}(A \cup B) \quad \text{ama} \quad 2 \notin \text{Int}(A) \cup \text{Int}(B) $$

Yani bu durumda dahil olma geçerli olsa da, eşitlik sağlanmaz:

$$ \text{Int}(A) \cup \text{Int}(B) \subsetneq \text{Int}(A \cup B) $$

3. Örnek: Kesişen Açık Diskler

\(\mathbb{R}^2\) düzleminde, kısmen kesişen iki açık diski düşünelim. Disklerden biri orijinde merkezlenmiş, diğeri ise $(0.5, 0)$ noktasında merkezlenmiştir:

$$ A = \{ (x, y) \mid x^2 + y^2 < 1 \} $$

$$ B = \{ (x, y) \mid (x - 0.5)^2 + y^2 < 1 \} $$

Açık kümeler oldukları için:

$$ \text{Int}(A) = A \quad \text{ve} \quad \text{Int}(B) = B $$

Dolayısıyla:

$$ \text{Int}(A) \cup \text{Int}(B) = A \cup B $$

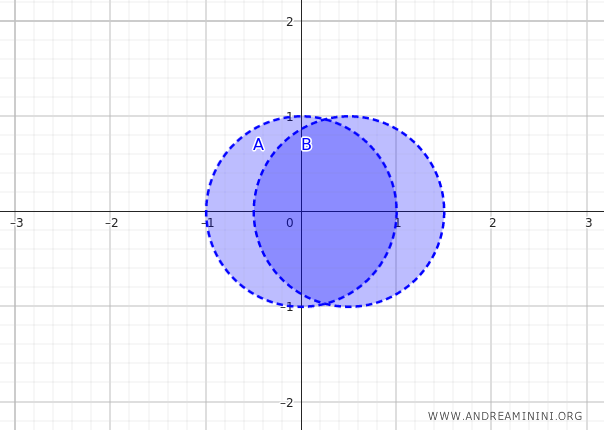
Birleşimin iç kümesi yine aynı bölgedir:

$$ \text{Int}(A \cup B) = A \cup B $$

Bu örnekte eşitlik sağlanır, çünkü her iki küme de açık olduğu için birleşimleri de açık bir kümedir.

Sonuç: Neden Bu Fark Önemlidir?

Bu örnekler, topolojide küçük ama önemli bir ayrımı gösterir. İki kümenin içlerinin birleşimi, daima birleşimlerinin iç kümesinin bir altkümesidir. Ancak eşitlik yalnızca bazı özel durumlarda gerçekleşir - genellikle kümelerin açık olması veya aralarında boşluk bulunmaması gerekir.

Bu fark, topolojide açıklık ve sınır kavramlarını doğru anlamak için kritik öneme sahiptir. Çünkü “iç” kavramı, bir noktanın çevresinin tamamen küme içinde kalıp kalmadığıyla ilgilidir. Kümeler arasında küçük bir sınır bile varsa, eşitlik hemen bozulur.

İspatın Özeti

İspat oldukça doğrudandır. Diyelim ki \( x \in \text{Int}(A) \cup \text{Int}(B) \). Bu, \( x \)’in ya \( A \)’nın ya da \( B \)’nin iç noktasında olduğunu gösterir. Eğer \( x \in \text{Int}(A) \) ise, \( x \)’in bir komşuluğu \( U_x \subseteq A \) vardır. Benzer şekilde \( x \in \text{Int}(B) \) ise, \( V_x \subseteq B \) komşuluğu bulunur.

Her iki durumda da, \( U_x \) veya \( V_x \) kümesi \( A \cup B \)’nin içinde kalır. Bu da \( x \)’in \( A \cup B \)’nin iç noktası olduğunu kanıtlar.

Böylece şu sonuç elde edilir:

$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$

ve ispat tamamlanır.

Kısa Özet

• İki kümenin içlerinin birleşimi, birleşimlerinin iç kümesinin içinde yer alır.
• Eşitlik yalnızca özel durumlarda (örneğin kümeler açık olduğunda) geçerlidir.
• Bu fark, topolojik kavramların inceliğini anlamak açısından temeldir.