Множества, не являющиеся ни открытыми, ни замкнутыми

В топологии существует особый тип множеств, которые не относятся ни к открытым, ни к замкнутым. Такие множества не удовлетворяют критериям ни одной из этих категорий.

Подобные ситуации возникают в тех топологических пространствах, где множество не объявлено открытым и одновременно не совпадает с дополнением открытого множества. В результате оно не является и замкнутым.

Примечание: В классической топологии действительных чисел такие случаи встречаются редко, что затрудняет их визуализацию. Однако в более общих топологических пространствах они являются естественными и часто встречающимися объектами. Рассмотрение конкретного примера помогает быстрее уловить суть.

Практический пример

Пусть X={a,b,c,d}, а топология T задается следующими открытыми множествами: {b}, {a,b}, {c,d}, {b,c,d}, {a,b,c,d} и Ø.

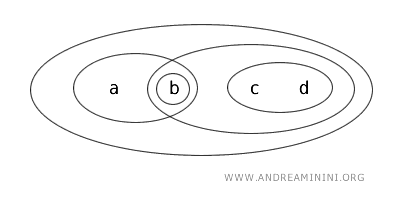
Рассмотрим подмножество {b,c} множества X.

• Множество {b,c} не является открытым, так как топология T не включает его в свой список открытых множеств.
• Оно также не является дополнением открытого множества в T, поэтому не может считаться замкнутым.

Итак, в топологии T множество {b,c} не относится ни к открытым, ни к замкнутым. Подобные примеры наглядно показывают, что в топологии встречаются ситуации, выходящие за пределы привычных интуитивных представлений.

И так далее.