정리: 열린집합과 닫힌집합으로 이해하는 연결공간
위상공간 \( X \)가 연결 공간(connected space)이라고 불리려면, \( X \) 안에서 동시에 열린(open) 집합이자 닫힌(closed) 집합인 부분집합(즉, 클로픈(clopen) 집합)이 오직 전체집합 \( X \)과 공집합 \( \emptyset \)뿐이어야 한다.
간단히 말해, 공간을 두 개의 서로소이면서 공집합이 아닌 열린집합으로 나눌 수 없다면 그 공간은 연결되어 있다. 이런 경우, 존재할 수 있는 클로픈 집합은 전체 공간과 공집합뿐이다.
이 정리는 위상적 연결성(topological connectedness)을 판단하는 데 매우 기본적이면서도 강력한 기준이다. 즉, 더 복잡한 개념인 호연결성(path connectedness)을 사용하지 않고도 공간의 연결 여부를 명확히 확인할 수 있다.
개념 이해
위상수학에서 어떤 부분집합이 동시에 열린집합이자 닫힌집합이라면, 그 집합은 공간을 분리(separation)하는 역할을 한다. 즉, 공간 \( X \)를 서로소인 두 개의 열린집합으로 나누는 것이다.
이러한 부분집합이 존재하면 공간은 두 개의 공집합이 아닌 열린집합의 합집합으로 표현될 수 있다. 따라서 그 공간은 비연결 공간(non-connected space) 또는 분리된 공간(disconnected space)이라고 한다.
반대로, \( X \) 안의 클로픈 집합이 전체집합 \( X \)과 공집합 \( \emptyset \)뿐이라면 공간을 나눌 방법이 존재하지 않는다. 이런 공간을 우리는 연결 공간이라고 부른다.
참고. 어떤 위상공간이든 전체집합 \( X \)과 공집합 \( \emptyset \)은 항상 동시에 열린집합이자 닫힌집합이다. 이 두 집합은 자명한 클로픈 집합의 대표적인 예이다.
예시 1: 유한한 비연결 공간
공간 \( X = \{ a, b, c, d \} \)에 대해, 열린집합이 \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \)로 정의된 위상 \( T \)를 생각해보자.
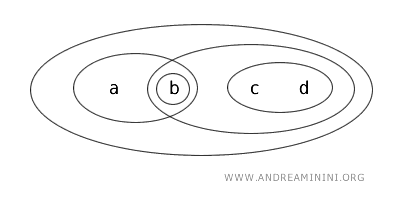
이때 부분집합 \( \{ a, b \} \)는 다음 이유로 클로픈 집합이다.
- \( \{ a, b \} \)는 위상 \( T \)의 열린집합이므로 열린집합이다.
- 그 여집합 \( X \setminus \{ a, b \} = \{ c, d \} \)도 열린집합이므로 닫힌집합이기도 하다.
따라서 위상공간 \( (X, T) \)는 비연결 공간이다. 공집합이 아닌 클로픈 집합이 하나라도 존재한다면 그 공간은 연결되어 있지 않다고 말할 수 있다.
실제로 \( \{ a, b \} \)와 \( \{ c, d \} \)는 서로소이고 공집합이 아닌 열린집합이므로, 공간을 이 둘로 분리할 수 있다. 따라서 이 공간은 위상적 연결성을 만족하지 않는다.
예시 2: 실수 직선
이번에는 실수 전체집합 \( \mathbb{R} \)을 생각해보자. 이 공간은 열린구간 \( (a, b) \)로 생성되는 표준 위상(standard topology)을 갖는다.
이 위상에서 \( (a, b) \)는 열린집합이지만 닫힌집합은 아니고, 반대로 \( [a, b] \)는 닫힌집합이지만 열린집합은 아니다.
결국 \( \mathbb{R} \) 안에서 동시에 열린집합이자 닫힌집합인 것은 전체집합 \( \mathbb{R} \)과 공집합 \( \emptyset \)뿐이다.
따라서 표준 위상을 가진 실수 직선 \( \mathbb{R} \)은 연결 공간이다.
예시 3: 실수의 비연결 부분공간
이번에는 부분공간 \( X = (0,1) \cup (2,3) \subset \mathbb{R} \)을 살펴보자. \( X \)는 실수의 표준 위상으로부터 부분위상(subspace topology)을 물려받는다.
이때 \( (0,1) \)과 \( (2,3) \)은 \( X \) 안에서 동시에 열린집합이자 닫힌집합이다. 이유는 간단하다. 각 구간의 여집합이 바로 다른 구간이기 때문이다.
- \( X \)에서 \( (0,1) \)의 여집합은 \( (2,3) \)이며, 이는 \( X \) 안에서 열린집합이다.
- \( X \)에서 \( (2,3) \)의 여집합은 \( (0,1) \)이며, 역시 열린집합이다.
따라서 두 구간 모두 클로픈 집합이다.
이처럼 자명하지 않은 클로픈 집합이 존재하므로, 부분공간 \( X \)는 비연결 공간이다.
즉, \( X \)는 두 개의 서로소이면서 공집합이 아닌 열린집합 \( (0,1) \)과 \( (2,3) \)으로 구성되어 있으며, 각각은 독립된 연결 성분(connected component)이다. 이 두 성분의 점들을 연속적인 위상적 경로로 연결할 수 없다는 사실이 바로 \( X \)가 연결되어 있지 않음을 보여준다.