부분집합의 열린 분리 이해하기

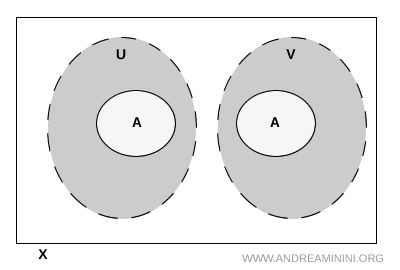
위상공간 $ X $ 안의 부분집합 $ A $를 생각해 보자. 열린 집합 $ U $와 $ V $가 아래 조건을 모두 만족한다면, 우리는 $ A $가 이 두 열린 집합에 의해 분리되었다고 말한다.

$ A $가 $ U \cup V $ 안에 완전히 포함된다 \[ A \subseteq U \cup V \]
두 집합 모두 $ A $와 실제로 접점을 가진다 \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
$ A $ 안에서 $ U $와 $ V $가 서로 겹치지 않는다 \[ U \cap V \cap A = \varnothing \]

요약하면, 부분집합 $ A $는 열린 집합 $ U $와 $ V $를 통해 명확하게 두 조각으로 나뉜다. 이 두 조각은 $ A $ 내부에서 서로 닿지 않기 때문에, $ A $가 어떻게 전체 공간 속에서 분리되어 있는지를 자연스럽게 보여 준다.

열린 집합에 의해 부분집합 A가 두 부분으로 나뉘는 구조를 설명하는 그림

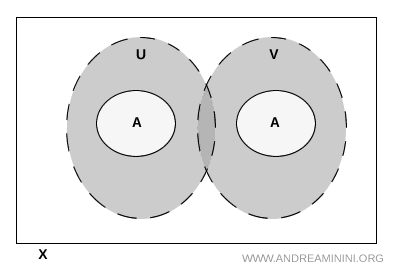
Nota. 열린 집합 $ U $와 $ V $는 전체 공간 $ X $에서 서로 떨어져 있을 필요는 없다. $ A $ 바깥에서는 겹칠 수도 있다. 핵심은 그 겹치는 부분이 $ A $에 닿지 않아야 한다는 점이다.
부분집합 A 외부의 영역에서는 U와 V가 교차할 수 있음을 보여 주는 그림

사례로 살펴보기

실제 예로 실수 직선 $ X = \mathbb{R} $을 떠올려 보자. 여기서 부분집합 $ A $는 서로 떨어진 두 닫힌 구간으로 이루어져 있다.

$$ A = [-2,-1] \cup [1,2] $$

이제 다음 두 열린 구간을 준비한다.

$$ U = (-3,0) $$

$$ V = (0,3) $$

이 구조는 아래 그림처럼 시각적으로도 바로 확인할 수 있다.

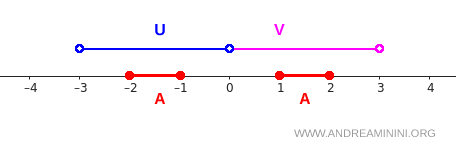
부분집합 A와 열린 집합 U, V의 위치 관계를 보여 주는 그래프

조건을 차근차근 확인해 보자.

먼저, 두 구간 가운데 $ [-2,-1] $은 전부 $ U $에 속하고, $ [1,2] $는 전부 $ V $에 속한다. 따라서 전체적으로

$$ A \subseteq U \cup V $$

가 성립한다.

다음으로 두 열린 집합 모두 $ A $와 실제로 만난다.

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

그리고 가장 중요한 조건인, $ A $ 내부에서의 비겹침을 확인해 보자.

$$ U \cap V \cap A = \varnothing $$

결과적으로 열린 집합 $ U $와 $ V $는 실수 직선 위에서 부분집합 $ A $를 깔끔하게 분리하고 있다. 이러한 분리는 위상수학에서 부분집합의 구조를 이해하는 데 중요한 기초 개념으로 널리 사용된다.