연결 공간 (Connected Space)
열린 집합으로 이해하는 연결성
위상 공간 $ X $가 연결(connected)되었다는 것은, 전체 공간을 두 개의 공집합이 아닌 서로소(open, disjoint) 열린 집합 $ U $, $ V $로 나눌 수 없다는 뜻이다.
- $ U \neq \emptyset $, $ V \neq \emptyset $ - 두 집합 모두 비어 있지 않다.
- $ U \cap V = \emptyset $ - 서로 겹치는 부분이 없다.
- $ U \cup V \ne X $ - 두 집합을 합쳐도 전체 공간을 덮지 못한다.
반대로 이런 열린 집합 쌍이 존재한다면, 그 공간은 비연결(disconnected)되었다고 한다.
즉, 공간을 둘로 나눌 수 없다면 연결, 나눌 수 있다면 비연결이다. 단순하면서도 강력한 개념이다.
이때 공집합이 아닌 서로소 열린 집합의 쌍 ( (U, V) )를 ( X )의 분리(separation)라고 부른다.
참고. 이것이 바로 열린 집합을 이용한 위상적 연결성(topological connectedness)의 정의이다. 이 개념은 우리가 자주 듣는 "경로 연결성(path connectedness)" 또는 "호 연결성(arc connectedness)"과는 다르며, 두 개념이 항상 일치하지는 않는다.
예시로 살펴보는 연결성과 비연결성
세 개의 점으로 이루어진 집합 $ X = {a, b, c} $를 생각해 보자. 이 집합에 다음 두 가지 위상을 정의할 수 있다.
- 위상 A
열린 집합의 모임: $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$ - 위상 B
열린 집합의 모임: $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$
두 공간 중 어떤 쪽이 연결되어 있을까?
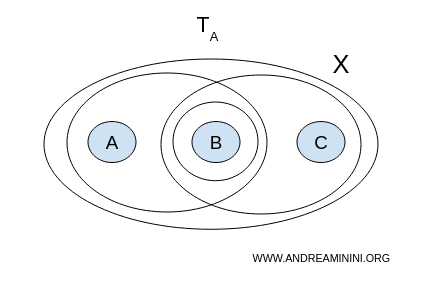
① 위상 A의 경우
위상 $ \mathcal{T}_A $ 안에서 공집합이 아닌 서로소 열린 집합 (U, V)을 찾아, 두 집합의 합이 $ X $ 전체를 덮는지 확인해 보자.
- $ U = {a,b}, V = {b,c} $ → $ b $를 공유하므로 서로소 아님.
- $ U = {a,b}, V = {b} $ → 서로소 아님.
- $ U = {b}, V = {b,c} $ → 서로소 아님.
결과적으로, 전체 $ X $를 덮는 공집합이 아닌 서로소 열린 집합 쌍은 존재하지 않는다.
따라서 위상 $ A $를 가진 공간 $ X $는 연결 공간이다.
② 위상 B의 경우
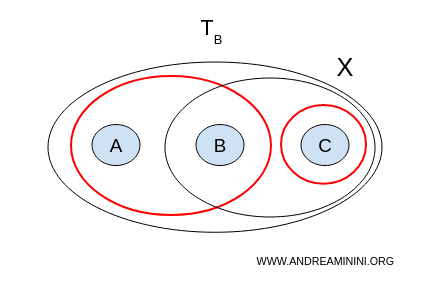
이번에는 위상 $ \mathcal{T}_B $에서 분리 $ (U, V) $가 존재하는지 살펴보자.
- $ U = {a,b}, V = {b,c} $ → $ b $를 공유하므로 서로소 아님.
- $ U = {a,b}, V = {c} $ → 서로소이며, 합집합은 $ X $ 전체를 덮는다: $ U \cup V = {a,b,c} = X $.
즉, 이 쌍 ( $ U = {a,b}, V = {c} $ )은 분리의 조건을 충족한다. 따라서 위상 B를 가진 공간 $ X $는 비연결 공간이다.
참고. 이 예시는 연결성이 단순히 점들의 모임에 의해 결정되는 것이 아니라, 어떤 위상을 택했는가에 따라 달라질 수 있음을 보여준다. 같은 집합이라도 위상 A에서는 연결이 유지되지만, 위상 B에서는 끊어진다.
실수 직선에서의 예시
실수 $ n $을 하나 고정하자. 다음과 같은 공간을 생각할 수 있다.
$$ X = (-\infty, n) \cup (n, +\infty) $$
이는 실수 직선에서 한 점 $ n $을 뺀 집합, 즉
$$ X = \mathbb{R} \setminus {n} $$
이다. 이 공간은 연결되어 있을까?
열린 집합 $ U = (-\infty, n) $, $ V = (n, +\infty) $를 살펴보면 다음과 같다.
- 두 집합 모두 표준 위상에서 열린 집합이다.
- 서로 교집합이 없다.
- 공집합이 아니다.
그리고 $ U \cup V = X $가 성립한다. 즉, 이 두 집합은 ( X )의 분리를 이룬다.
따라서 공간 $ X = (-\infty, n) \cup (n, +\infty) $는 비연결 공간이다.
참고. 실수 직선에서 한 점을 제거하면, 선이 그 지점에서 끊어져 왼쪽과 오른쪽이 완전히 분리된다. 이 두 부분을 잇는 연속적인 경로는 존재하지 않으므로, 이 공간은 위상적으로 비연결이며 동시에 경로 연결성(path-connected)도 갖지 않는다.
연결성과 경로 연결성의 차이
연결성과 경로 연결성은 비슷해 보이지만, 실제로는 다르다.
어떤 공간은 연결되어 있지만 경로로 이어질 수 없을 수도 있다.
- 위상적 연결성: 공간을 두 개의 공집합이 아닌 서로소 열린 부분집합으로 나눌 수 없다.
- 경로 연결성: 공간 안의 임의의 두 점을 그 공간 안에서 완전히 포함되는 연속적인 경로로 연결할 수 있다. 이 경로가 같은 점을 두 번 지나지 않으면 호 연결(arc-connected)이라 한다.
모든 경로 연결 공간은 연결되어 있지만, 모든 연결 공간이 경로 연결인 것은 아니다.
연속적인 경로가 존재한다면 공간은 "끊어지지 않은 하나의 덩어리"로 유지된다. 하지만 연결되어 있다고 해서 반드시 경로로 이동할 수 있는 것은 아니다.
예시. 대표적인 반례는 위상수학자의 사인 곡선(topologist's sine curve)이다: $$ S = { (x, \sin(1/x)) \mid x > 0 } \cup { (0, y) \mid -1 \le y \le 1 } $$ 이 공간은 두 개의 열린 집합으로 나눌 수 없으므로 연결되어 있지만, 진동하는 곡선과 세로선의 점들을 잇는 연속적인 경로가 존재하지 않아 경로 연결되지 않는다.
이처럼 연결성과 경로 연결성의 차이를 이해하면, 공간의 구조와 성질을 보다 깊이 파악할 수 있다.
참고
연결 공간에 대한 추가 설명
- 정리: 열린집합과 닫힌집합(클로픈 집합)을 통한 연결공간의 특징
위상공간 \( X \)가 연결 공간(connected space)이라는 것은, \( X \) 안에서 동시에 열린(open) 집합이자 닫힌(closed) 집합인 부분집합(즉, 클로픈 집합(clopen set))이 전체집합 \( X \)과 공집합 \( \emptyset \)뿐일 때를 의미한다.
이 정리는 연결성의 개념을 이해하는 데 있어 기본적이면서도 매우 중요한 출발점이 된다. 이후의 내용에서 연결성과 관련된 보다 구체적인 성질과 응용을 살펴본다.