공통점을 통한 연결성

위상공간 \( X \)에서 연결된 부분집합들의 모임 \( C_1, C_2, \dots, C_n \subset X \)이 적어도 하나의 공통점을 가진다고 하자. 즉, \[
\bigcap_{i=1}^n C_i \neq \varnothing \] 라고 가정한다. 이때 이들의 합집합 \( \bigcup_{i=1}^n C_i \)는 하나의 연결 집합이 된다.

다시 말해, 두 개 이상의 연결된 부분집합이 하나 이상의 점을 공유한다면, 그 전체를 합친 집합 역시 끊어지지 않고 하나로 이어진다.

이 성질은 모든 집합이 공통으로 포함하는 점이 존재한다는 사실에 근본적으로 의존한다.

Note. 조건 \( \bigcap_{i=1}^n C_i \neq \varnothing \)는 합집합 \( \bigcup_{i=1}^n C_i \)가 연결되기 위한 충분조건이지만, 필요조건은 아니다. 즉, 모든 집합이 동일한 점을 공유하지 않더라도, 경우에 따라 합집합은 여전히 연결될 수 있다. 예를 들어, 집합들이 사슬처럼 연속적으로 겹쳐 있는 경우가 이에 해당한다.

구체적인 예

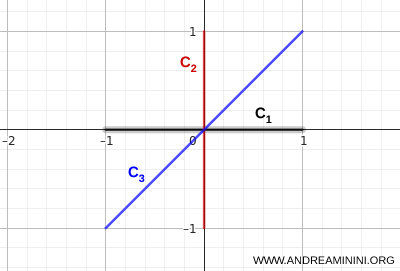
다음과 같은 \( \mathbb{R}^2 \)의 부분집합들을 생각해 보자.

• \( C_1 \): \( (-1,0) \)에서 \( (1,0) \)까지의 수평 선분
• \( C_2 \): \( (0,-1) \)에서 \( (0,1) \)까지의 수직 선분
• \( C_3 \): \( (-1,-1) \)에서 \( (1,1) \)을 잇는 대각선 선분

이들 각각은 연결 집합이다.

또한 이 세 선분은 모두 점 \( (0,0) \)을 지난다. 즉,

\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]

따라서 이들의 공통 교집합은 공집합이 아니다.

\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]

이로부터, 연결성에 대한 기준에 따라 다음이 성립한다.

\[ C_1 \cup C_2 \cup C_3 \]

즉, 세 선분의 합집합은 하나의 연결된 집합이다.

세 선분은 모두 동일한 중심점에서 만난다. 이로 인해 전체 구조는 끊어지지 않고 하나로 이어진다.

이 집합 안에서는 어느 한 점에서 출발하더라도, 집합 내부만을 따라 이동하여 다른 임의의 점에 도달할 수 있다.

Note. 모든 \( C_i \)가 반드시 공통점을 가져야만 합집합이 연결되는 것은 아니다. 예를 들어, 각 집합이 사슬처럼 서로 겹치며 이어지는 경우, 즉 \( C_i \cap C_{i+1} \neq \varnothing \)가 성립하면 전체 합집합 \( \bigcup_i C_i \)는 여전히 연결된다. 더 나아가, 일부 집합들 사이에 직접적인 교차가 없더라도, 다른 집합들이 이를 이어 주는 역할을 하면 전체는 연결 상태를 유지한다. 예를 들어 세 개의 선분이 삼각형을 이루는 경우를 생각해 보자. 이때 전체 교집합은 공집합이지만, \( \bigcap_i C_i = \varnothing \), 그럼에도 불구하고 합집합은 연결 집합이다.

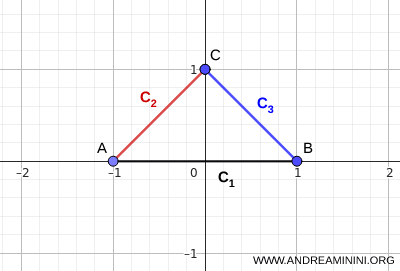
이 예시는 사슬 구조가 연결성을 보장할 수 있음을 직관적으로 보여준다.

증명

위상공간 \( X \)에서, 공통 교집합이 공집합이 아닌 연결 부분집합들의 족 \( \{C_i\}_{i \in I} \)를 생각하자.

\[ \bigcap_{i \in I} C_i \neq \varnothing \]

이제 다음과 같이 합집합을 정의한다.

\[ C = \bigcup_{i \in I} C_i \]

이 집합이 연결이 아니라고 가정하자.

그렇다면 \( C \)는 두 개의 서로 분리된 열린집합 \( U \), \( V \)로 나뉜다. 즉, 다음이 성립한다.

• \( U \cap C \neq \varnothing \)
• \( V \cap C \neq \varnothing \)
• \( (U \cap C) \cap (V \cap C) = \varnothing \)
• \( C = (U \cap C) \cup (V \cap C) \)

가정에 의해 모든 \( C_i \)의 교집합은 공집합이 아니므로,

\[ \bigcap_{i \in I} C_i \neq \varnothing \]

어떤 점 \( x \in C \)가 존재하여 모든 \( C_i \)에 속한다.

\[ x \in \bigcap_{i \in I} C_i \]

이 점은 분리의 정의에 따라 \( U \) 또는 \( V \) 중 하나에 속해야 하며, 동시에 둘 모두에 속할 수는 없다. 일반성을 잃지 않고 다음과 같이 가정하자.

\[ x \in U \quad \text{이고} \quad x \notin V \]

각각의 \( C_i \subset C \)에 대해 다음이 성립한다.

\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]

\( C_i \cap U \)와 \( C_i \cap V \)는 부분공간 위상에서 열린 집합이며, 서로소이고, 그 합은 \( C_i \) 전체를 이룬다. 그런데 각 \( C_i \)는 연결 집합이므로, 이 둘 중 하나는 반드시 공집합이어야 한다.

따라서 각 \( C_i \)는 전부 \( U \) 또는 \( V \) 중 하나에 포함된다.

\[ C_i \subset U \quad \text{또는} \quad C_i \subset V \]

그런데 \( x \in C_i \)이고 \( x \in U \)이므로, \( C_i \subset V \)일 수는 없다.

따라서 모든 \( i \in I \)에 대해 다음이 성립한다.

\[ C_i \subset U \]

결국 합집합 전체가 \( U \)에 포함된다.

\[ \bigcup_{i \in I} C_i \subset U \]

이는 \( V \cap C \neq \varnothing \)라는 가정과 모순이다.

따라서 처음의 가정은 거짓이며, 결론적으로 \( \bigcup_{i \in I} C_i \)는 연결 집합이다.

이로써 증명이 완결된다.