열린집합을 이용한 연결되지 않음의 특징

위상공간 $X$의 부분집합 $A$가 연결되지 않았다는 것은 $X$ 안에서 $A$를 두 부분으로 완전히 나누는 열린집합 $U$와 $V$가 존재한다는 뜻이다. 이 열린집합들은 다음 조건을 만족한다.

이 조건들은 열린집합만을 사용해 $A$의 연결 여부를 판단할 수 있게 해 준다. 연결되지 않은 집합은 항상 서로 겹치지 않는 두 열린집합을 통해 자연스럽게 분리된다.

예 1. 떨어져 있는 두 구간

다음 집합을 실수직선에서 생각해 보자.

$$ A = [0,1] \cup [2,3] $$

두 구간이 분명히 떨어져 있으므로 직관적으로도 연결되지 않았다.

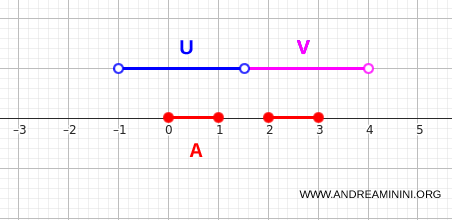
실수축에서 분리된 구간 예시

이를 열린집합으로 표현하면 다음과 같다.

두 집합은 각각 $A$의 한 구간과 교차하고, 서로 겹치지 않는다.

$$ U \cap A = [0,1], \qquad V \cap A = [2,3] $$

$$ (U \cap V) \cap A = \varnothing $$

따라서 $U$와 $V$는 $A$를 자연스럽게 둘로 나누며 $A$가 연결되지 않았음을 확인시켜 준다.

이번에는 다음 집합을 보자.

$$ A = \{1, 3\} $$

두 점 사이를 $A$ 내부에서 잇는 방법이 전혀 없기 때문에 이 집합 역시 연결되지 않았다.

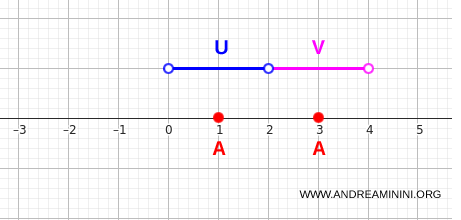
실수축에서 분리된 두 점

열린구간을 사용하면 간단히 확인된다.

$$ U = (0,2), \qquad V = (2,4) $$

각 열린집합은 $A$의 한 점씩만 포함하고 서로 겹치지 않는다.

$$ U \cap A = \{1\}, \qquad V \cap A = \{3\} $$

$$ U \cap V \cap A = \varnothing $$

이처럼 아주 단순한 경우에도 열린집합을 통해 연결 여부를 정확히 판단할 수 있다.

이번에는 2차원 평면에서 전체 $x$축을 제거한 다음 집합을 생각해 보자.

$$ A = \{(x,y): y > 0\} \cup \{(x,y): y < 0\} $$

위반평면과 아래반평면은 서로 닿을 수 없기 때문에 이 집합은 연결될 수 없다.

열린집합을 이용하면 다음과 같다.

$$ U = \{(x,y): y > -1\}, \qquad V = \{(x,y): y < 1\} $$

두 열린집합의 공통 부분은 $A$와 만나지 않는다.

$$ (U \cap V) \cap A = \varnothing $$

이 예시 역시 열린집합만으로 연결되지 않음을 명확히 보여 준다.

연결은 위상수학에서 매우 기본적이면서 중요한 개념이다. 공간이 한 덩어리로 이루어져 있는지, 혹은 여러 조각으로 갈라져 있는지를 판단하는 기준이 되기 때문이다. 특히 열린집합을 통해 연결 여부를 판정할 수 있다는 점은 위상적 구조를 분석하는 데 큰 장점을 제공한다.

이 관점은 연결 개념을 더욱 직관적으로 이해하게 해 주며, 다양한 위상적 구조를 분석할 때 기본 도구로 널리 사용된다.