Teorema: karakterisasi ruang terhubung melalui himpunan terbuka dan tertutup

Dalam topologi, sebuah ruang \( X \) disebut terhubung jika dan hanya jika satu-satunya subhimpunan dari \( X \) yang sekaligus terbuka dan tertutup (disebut juga clopen) adalah seluruh ruang \( X \) itu sendiri dan himpunan kosong \( \emptyset \).

Artinya, suatu ruang dikatakan terhubung apabila tidak bisa dipisahkan menjadi dua bagian terbuka yang saling lepas dan keduanya tidak kosong. Dalam situasi seperti ini, hanya ada dua himpunan clopen yang mungkin: seluruh ruang dan himpunan kosong.

Teorema ini memberikan cara yang sederhana namun kuat untuk memahami keterhubungan topologis. Dengan kriteria ini, kita bisa menentukan apakah suatu ruang bersifat terhubung tanpa harus menggunakan konsep yang lebih kompleks seperti keterhubungan lintasan (path connectedness).

Memahami idenya

Subhimpunan yang sekaligus terbuka dan tertutup pada dasarnya memisahkan ruang menjadi dua bagian terbuka yang saling lepas dan tidak kosong. Jika subhimpunan semacam itu ada, maka ruang dapat dianggap “terbelah” menjadi dua bagian yang terpisah, sehingga ruang tersebut tidak terhubung.

Sebaliknya, jika satu-satunya himpunan clopen yang ada hanyalah seluruh ruang dan himpunan kosong, maka tidak ada cara untuk membagi ruang itu tanpa merusak strukturnya. Dengan kata lain, ruang tersebut terhubung secara topologis.

Catatan. Dalam setiap ruang topologi, himpunan total \( X \) dan himpunan kosong \( \emptyset \) selalu bersifat clopen. Keduanya merupakan contoh dasar yang bersifat trivial.

Contoh 1: ruang hingga yang tidak terhubung

Pertimbangkan ruang \( X = \{ a, b, c, d \} \) dengan topologi \( T \) yang ditentukan oleh himpunan-himpunan terbuka berikut: \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \).

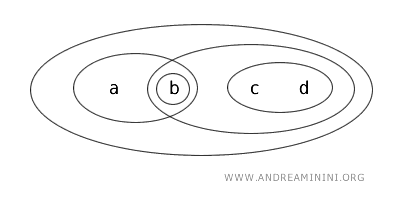
Pada contoh ini, subhimpunan \( \{ a, b \} \) bersifat clopen karena:

• ia terbuka, sebab termasuk dalam koleksi himpunan terbuka dari topologi \( T \);
• ia juga tertutup, karena komplemennya \( X \setminus \{ a, b \} = \{ c, d \} \) merupakan himpunan terbuka dalam \( T \).

Dari sini kita tahu bahwa ruang topologi \( (X, T) \) tidak terhubung, karena memiliki subhimpunan sejati yang clopen dan tidak kosong. Satu saja himpunan clopen non-trivial sudah cukup untuk membuktikan bahwa ruang tersebut tidak terhubung.

Faktanya, keberadaan himpunan seperti \( \{ a, b \} \) dan \( \{ c, d \} \) menunjukkan bahwa ruang ini dapat ditulis sebagai gabungan dua himpunan terbuka yang saling lepas dan tidak kosong. Maka syarat keterhubungan topologis tidak terpenuhi.

Contoh 2: garis bilangan real

Sekarang perhatikan himpunan bilangan real \( \mathbb{R} \) dengan topologi standar yang dibentuk oleh interval terbuka \( (a, b) \).

Dalam topologi ini, setiap interval \( (a, b) \) adalah terbuka namun tidak tertutup, sementara interval \( [a, b] \) adalah tertutup namun tidak terbuka.

Satu-satunya himpunan yang sekaligus terbuka dan tertutup di \( \mathbb{R} \) hanyalah \( \mathbb{R} \) sendiri dan \( \emptyset \). Karena itu, garis bilangan real dengan topologi standar merupakan ruang yang terhubung.

Contoh 3: subruang yang tidak terhubung dari \( \mathbb{R} \)

Pertimbangkan subruang \( X = (0,1) \cup (2,3) \subset \mathbb{R} \) dengan topologi subruang (subspace topology) yang diturunkan dari topologi standar pada \( \mathbb{R} \).

Dalam kasus ini, kedua interval \( (0,1) \) dan \( (2,3) \) sekaligus terbuka dan tertutup dalam \( X \), karena komplemen masing-masing di dalam \( X \) adalah interval yang lain. Secara rinci:

• komplemen dari \( (0,1) \) dalam \( X \) adalah \( (2,3) \), yang terbuka dalam \( X \);
• komplemen dari \( (2,3) \) dalam \( X \) adalah \( (0,1) \), yang juga terbuka dalam \( X \).

Kedua subhimpunan ini bersifat clopen, sehingga \( X \) merupakan ruang yang tidak terhubung.

Dengan kata lain, \( X \) terdiri atas dua komponen terhubung (connected components) yang terpisah, yaitu \( (0,1) \) dan \( (2,3) \). Keduanya terbuka, tidak kosong, dan tidak saling beririsan. Tidak ada cara untuk menghubungkan titik dari satu komponen ke titik di komponen lainnya melalui jalur kontinu, dan inilah yang menjadi ciri khas ruang topologi yang tidak terhubung.