Ruang Terhubung dalam Topologi

Memahami konsep keterhubungan melalui himpunan terbuka

Dengan kata lain, sebuah ruang dikatakan terhubung secara topologis bila tidak bisa dipisahkan menjadi dua bagian terbuka yang terpisah dan tidak kosong. Ruang yang dapat dibagi menjadi dua bagian terbuka seperti itu disebut tidak terhubung, dan pasangan ( (U, V) ) yang memisahkannya disebut pemisahan dari ( X ).

Catatan. Ini adalah definisi formal keterhubungan topologis berdasarkan himpunan terbuka. Seperti akan kita lihat, konsep ini tidak sama dengan keterhubungan lintasan atau keterhubungan busur - meskipun sering kali keduanya berhubungan erat.

Contoh sederhana untuk memahami konsep

Bayangkan himpunan $ X $ yang terdiri atas tiga elemen:

$$ X = {a, b, c} $$

Kita definisikan dua topologi yang berbeda di atas himpunan ini:

• Topologi A
  Himpunan terbukanya: $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$
• Topologi B
  Himpunan terbukanya: $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$

Pertanyaannya: manakah di antara kedua ruang ini yang benar-benar terhubung?

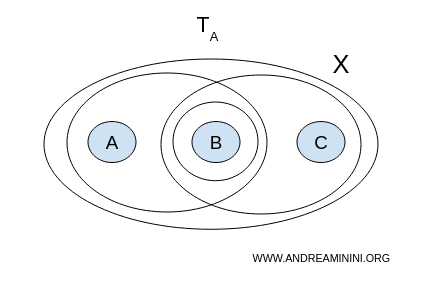
Kasus 1 - Topologi A

Kita cari apakah ada pasangan $ (U, V) $ dari himpunan terbuka dalam $ \mathcal{T}_A $ yang memenuhi syarat-syarat pemisahan, yaitu tidak kosong, saling terpisah, dan jika digabungkan menutupi seluruh ruang $ X $.

• $ U = {a,b}, V = {b,c} $ tidak saling terpisah karena keduanya memuat $ b $;
• $ U = {a,b}, V = {b} $ juga tidak terpisah;
• $ U = {b}, V = {b,c} $ pun tidak terpisah.

Tidak ada pasangan himpunan terbuka yang memenuhi semua syarat tersebut.

Jadi, dengan topologi $ A $, ruang topologi $ X $ adalah terhubung.

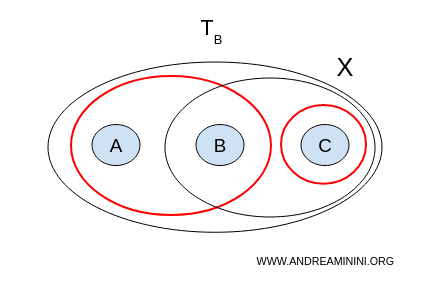
Kasus 2 - Topologi B

Sekarang, periksa topologi $ \mathcal{T}_B $.

• $ U = {a,b}, V = {b,c} $ tidak terpisah karena keduanya mengandung $ b $;
• $ U = {a,b}, V = {c} $ tidak kosong, saling terpisah, dan gabungannya menutupi seluruh ruang: $ U \cup V = {a,b,c} = X $.

Pasangan terakhir ini memenuhi semua syarat pemisahan. Maka, ruang $ X $ dengan topologi B adalah tidak terhubung.

Catatan. Contoh ini menunjukkan bahwa sifat keterhubungan tidak hanya bergantung pada himpunan titiknya, tetapi juga pada topologi yang digunakan. Dengan himpunan yang sama, dua topologi bisa menghasilkan struktur global yang sangat berbeda: satu menjaga keterhubungan, sementara yang lain memutuskannya.

Contoh lain di garis bilangan real

Sekarang pertimbangkan ruang $ X $ yang terdiri dari garis bilangan real tanpa satu titik $ n $ (misalnya $ n = 0 $):

$$ X = (-\infty, n) \cup (n, +\infty) $$

Ruang ini dapat dipandang sebagai garis real yang "terputus" di titik $ n $:

$$ X = \mathbb{R} \setminus {n} $$

Apakah ruang ini masih terhubung?

Ambil dua himpunan:

• $ U = (-\infty, n) $ dan $ V = (n, +\infty) $;
• Keduanya terbuka dalam topologi standar $ \mathbb{R} $;
• Keduanya tidak kosong dan saling terpisah.

Gabungan keduanya menutupi seluruh ruang $ X $:

$$ U \neq \emptyset, \quad V \neq \emptyset, \quad U \cap V = \emptyset, \quad U \cup V = X $$

Dengan demikian, ruang $ X = (-\infty, n) \cup (n, +\infty) $ adalah tidak terhubung, karena dapat dipisahkan menjadi dua bagian terbuka yang terpisah dan tidak kosong.

Catatan. Menghapus satu titik dari garis real membuat garis tersebut "terbelah" menjadi dua bagian - kiri dan kanan - yang tidak bisa disambungkan lagi oleh lintasan kontinu. Maka, ruang ini bukan hanya tidak terhubung secara topologis, tetapi juga tidak terhubung lintasan.

Perbedaan antara ruang terhubung dan terhubung lintasan

Keterhubungan topologis dan keterhubungan lintasan sering kali dianggap sama, padahal sebenarnya berbeda.

Sebuah ruang topologi bisa saja terhubung, tetapi tidak selalu terhubung lintasan.

• Keterhubungan topologis:
  Ruang tidak dapat dibagi menjadi dua himpunan terbuka yang saling terpisah dan tidak kosong.
• Keterhubungan lintasan:
  Setiap pasangan titik dalam ruang dapat dihubungkan oleh lintasan kontinu di dalam ruang tersebut. Jika lintasan itu tidak memotong dirinya sendiri, ruangnya disebut terhubung busur.

Secara umum, setiap ruang yang terhubung lintasan pasti terhubung, tetapi tidak semua ruang terhubung adalah terhubung lintasan.

Lintasan kontinu antara dua titik menjamin ruang tidak dapat "terbelah" menjadi dua wilayah terbuka yang terpisah. Namun, kebalikannya tidak selalu benar - ada ruang yang tetap terhubung tetapi tidak memiliki lintasan kontinu antara setiap pasangan titik.

Contoh menarik: Kurva sinus ahli topologi $$ S = { (x, \sin(1/x)) \mid x > 0 } \cup { (0, y) \mid -1 \le y \le 1 } $$ Kurva ini bersifat terhubung karena tidak dapat dipisahkan menjadi dua himpunan terbuka yang terpisah. Namun, ia tidak terhubung lintasan karena tidak ada lintasan kontinu yang bisa menghubungkan titik pada bagian kurva berosilasi dengan titik pada segmen vertikal.

Contoh ini menunjukkan betapa menarik dan kaya konsep keterhubungan dalam topologi - sebuah ide sederhana yang membuka banyak pintu untuk memahami struktur ruang yang lebih kompleks.

Catatan

Beberapa penjelasan tambahan mengenai ruang terhubung:

• Teorema: Karakterisasi Ruang Terhubung melalui Himpunan Terbuka dan Tertutup (Clopen)
  Sebuah ruang topologi \( X \) disebut terhubung apabila dan hanya apabila satu-satunya subhimpunan dari \( X \) yang sekaligus terbuka dan tertutup (clopen) adalah seluruh ruang \( X \) itu sendiri dan himpunan kosong \( \emptyset \).

Penjelasan serupa juga dapat diterapkan pada berbagai contoh lain dalam topologi yang melibatkan konsep keterhubungan dan pemisahan ruang.