Karakterisasi Himpunan Tak Terhubung melalui Himpunan Terbuka dalam Ruang Topologi

Secara sederhana, sebuah himpunan dinyatakan tak terhubung jika elemen-elemennya dapat dipisahkan secara bersih oleh dua himpunan terbuka yang tidak saling tumpang tindih pada bagian mana pun dari \(A\). Pendekatan ini menawarkan cara yang langsung dan efektif untuk mengenali ketakterhubungan hanya dengan melihat struktur terbuka ruang tersebut, tanpa perlu membawa konsep-konsep lanjutan.

Contoh ilustratif

Pertimbangkan himpunan berikut:

$$ A = [0,1] \cup [2,3] \subset \mathbb{R} $$

Dua interval tertutup ini tampak jelas terpisah. Tidak ada jalur di dalam \(A\) yang memungkinkan kita bergerak dari interval pertama ke interval kedua tanpa keluar dari himpunan.

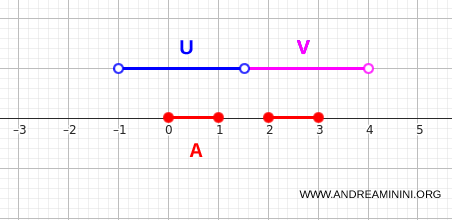
Kita dapat mengonfirmasi hal tersebut dengan memilih dua himpunan terbuka yang menaungi masing-masing interval:

• \(U = (-1,1.5)\)
• \(V = (1.5,4)\)

Keduanya beririsan dengan \(A\) dalam bagian tak kosong dan tidak memiliki titik bersama dalam \(A\):

$$ U \cap A = [0,1] $$

$$ V \cap A = [2,3] $$

$$ (U \cap V) \cap A = \varnothing $$

Dalam kerangka topologi, kondisi ini sudah memadai untuk menyimpulkan bahwa \(A\) tak terhubung.

Contoh 2: himpunan kecil yang tetap tak terhubung

Sekarang perhatikan himpunan yang jauh lebih sederhana:

$$ A = \{1, 3\} \subset \mathbb{R} $$

Meskipun hanya dua titik, mereka berada cukup jauh sehingga tidak mungkin terhubung satu sama lain dalam kerangka \(A\) itu sendiri.

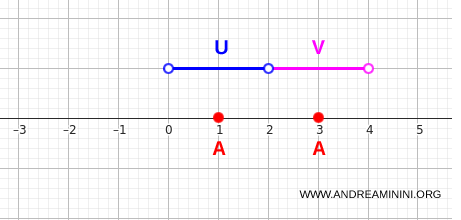
Kita dapat memisahkannya dengan mudah:

$$ U = (0,2) \qquad V = (2,4) $$

Hasilnya:

$$ U \cap A = \{1\} $$

$$ V \cap A = \{3\} $$

$$ U \cap V \cap A = \varnothing $$

Dengan demikian, bahkan himpunan kecil sekalipun dapat bersifat tak terhubung.

Contoh 3: dua semiplane dalam \(\mathbb{R}^2\)

Contoh berikut berada di dimensi dua. Pertimbangkan \(\mathbb{R}^2\) tanpa sumbu \(x\):

$$ A = \{(x,y) : y>0\} \cup \{(x,y) : y<0\} $$

Semiplane atas dan semiplane bawah pada dasarnya sudah terpisah oleh garis \(y = 0\), sehingga tidak ada hubungan topologis antara keduanya.

Pilih dua himpunan terbuka yang sesuai:

$$ U = \{(x,y) : y> -1\} $$

$$ V = \{(x,y) : y< 1\} $$

• \(U \cap A\) mencakup seluruh semiplane atas
• \(V \cap A\) mencakup seluruh semiplane bawah

Karena tidak ada elemen \(A\) yang berada pada irisan \(U \cap V\), pemisahan keduanya bersifat sempurna.

Pembuktian

Pembuktian formal dari karakterisasi ini berjalan dalam dua arah: jika himpunan dapat dipisahkan oleh himpunan terbuka, maka ia tak terhubung. Sebaliknya, jika ia memang tak terhubung, pemisahan semacam itu selalu dapat ditemukan.

A] Jika dua himpunan terbuka dapat memisahkan \(A\), maka \(A\) tak terhubung

Misalkan terdapat himpunan terbuka \(U\) dan \(V\) yang memenuhi syarat. Definisikan:

\[ P = U \cap A, \qquad Q = V \cap A \]

Keduanya memenuhi:

• tidak kosong,
• terbuka dalam topologi subruang,
• saling terpisah,
• dan bersama-sama menutupi seluruh \(A\).

Sifat-sifat ini tepat membentuk pemisahan, sehingga \(A\) tak terhubung.

B] Jika \(A\) tak terhubung, maka terdapat dua himpunan terbuka yang memisahkannya

Jika \(A\) tak terhubung, terdapat dua subhimpunan \(P\) dan \(Q\) dalam \(A\) yang membentuk pemisahan. Karena keduanya terbuka dalam topologi subruang, masing-masing dapat dituliskan sebagai irisan antara \(A\) dan sebuah himpunan terbuka ruang induk. Dengan demikian terdapat himpunan terbuka \(U\) dan \(V\) dalam \(X\) sehingga:

\[ P = U \cap A, \qquad Q = V \cap A \]

Kondisi ini memastikan bahwa \(U\) dan \(V\) memenuhi syarat karakterisasi.

C] Kesimpulan

Himpunan \(A\) dalam ruang topologi \(X\) bersifat tak terhubung jika dan hanya jika ia dapat dibagi menjadi dua bagian yang tak kosong, saling terpisah, dan terbuka sebagai subruang, yang berasal dari dua himpunan terbuka dalam ruang induk. Pemahaman ini memberikan cara yang ringkas dan langsung untuk mengenali struktur yang tidak terhubung hanya melalui himpunan terbuka.