Setiap himpunan terhubung terkandung dalam satu komponen terhubung
Misalkan \( A \) dan \( B \) adalah subhimpunan dari suatu ruang topologi \( X \), dengan \( A \) merupakan himpunan terhubung dan \( A \subset B \). Jika \( B \) dapat dipisahkan menjadi dua subhimpunan \( B_1 \) dan \( B_2 \) di dalam \( X \), maka \( A \) harus seluruhnya terkandung tepat di salah satu dari kedua subhimpunan tersebut: $$ A \subset B_1 \quad \text{atau} \quad A \subset B_2 $$
Intinya, sebuah himpunan terhubung tidak mungkin sekaligus beririsan dengan kedua bagian dari suatu pemisahan.
Apabila sebuah himpunan terhubung berada di dalam himpunan yang terbelah menjadi dua subhimpunan yang saling lepas, maka himpunan tersebut harus sepenuhnya berada di salah satu bagian itu.
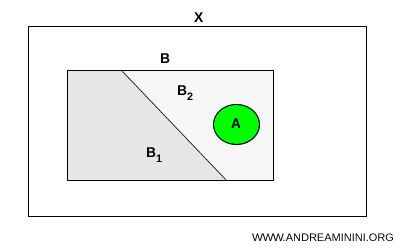
Secara intuitif, bayangkan sebuah himpunan terhubung seperti seutas tali yang masih utuh dan diletakkan di dalam sebuah amplop. Jika amplop tersebut dibagi menjadi dua kompartemen yang terpisah, sementara talinya tidak putus, maka tali itu pasti berada sepenuhnya di dalam salah satu kompartemen. Jika tidak, berarti talinya harus terputus. Dengan cara yang sama, sifat keterhubungan mencegah suatu himpunan untuk melintasi sebuah pemisahan.
Contoh konkret
Sebagai contoh, perhatikan ruang topologi berikut:
$$ X = \mathbb{R} $$
dan subhimpunan berikut dari \( X \):
$$ B = (-3,4) $$
Himpunan \( B \) ini dapat dipisahkan menjadi dua subhimpunan:
$$ B_1 = (-3,0) $$
$$ B_2 = (0,4) $$
Kedua subhimpunan tersebut saling lepas:
$$ B_1 \cap B_2 = \varnothing $$
dan gabungannya tepat membentuk kembali himpunan \( B \):
$$ B_1 \cup B_2 = B $$
Selain itu, \( B_1 \) dan \( B_2 \) merupakan himpunan terbuka dalam topologi subruang pada \( B \).
Dengan demikian, \( B_1 \) dan \( B_2 \) membentuk suatu pemisahan dari \( B \) di dalam \( X \).
Sekarang perhatikan subhimpunan terhubung berikut dari \( B \):
$$ A = (1,2) $$
Karena \( A \subset B_2 \), maka jelas bahwa \( A \) sepenuhnya berada di dalam salah satu bagian dari pemisahan tersebut.
Catatan. Jika, sebagai perbandingan, kita mengambil \( A = (-1,1) \), maka akan diperoleh $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ Keadaan ini tidak dapat terjadi. Alasannya, \( B_1 \) dan \( B_2 \) membentuk suatu pemisahan dari \( B \), sehingga sebuah subhimpunan terhubung dari \( B \) tidak boleh tersebar di kedua bagian tersebut. Jika hal ini dimungkinkan, maka \( A \) sendiri akan terpisah, yang bertentangan dengan fakta bahwa interval \( (-1,1) \) adalah himpunan terhubung. Masalahnya bukan pada keterhubungan interval tersebut, melainkan pada ketidakmungkinannya untuk terkandung di dalam \( B \) yang telah dipisahkan dengan cara ini.
Bukti
Asumsi
Misalkan \( A \) dan \( B \) adalah subhimpunan dari suatu ruang topologi \( X \), sehingga
$$ A \subset X \quad \text{dan} \quad B \subset X $$
dan anggap bahwa:
- \( A \) adalah himpunan terhubung
- \( A \subset B \)
- \( B_1 \) dan \( B_2 \) membentuk suatu pemisahan dari \( B \) di dalam \( X \)
Pernyataan
Dari asumsi-asumsi tersebut, berlaku bahwa \( A \) harus merupakan subhimpunan dari salah satu di antara \( B_1 \) atau \( B_2 \):
$$ A \subset B_1 \quad \text{atau} \quad A \subset B_2 $$
Bukti
Karena \( B_1 \) dan \( B_2 \) membentuk suatu pemisahan dari \( B \) di dalam \( X \), maka berlaku sifat-sifat berikut:
- \( B_1 \cap B_2 = \varnothing \), sehingga \( B_1 \) dan \( B_2 \) saling lepas
- \( B = B_1 \cup B_2 \), sehingga gabungan keduanya adalah seluruh \( B \)
- \( B_1 \) dan \( B_2 \) merupakan himpunan terbuka dalam topologi subruang pada \( B \)
Misalkan, untuk memperoleh kontradiksi, bahwa \( A \) tidak sepenuhnya terkandung di dalam \( B_1 \) maupun di dalam \( B_2 \). Dengan kata lain, anggap bahwa
$$ A \cap B_1 \neq \varnothing \qquad \text{dan} \qquad A \cap B_2 \neq \varnothing $$
Karena \( A \subset B \), maka berlaku
$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$
Selain itu, karena \( B_1 \) dan \( B_2 \) saling lepas, maka himpunan \( A \cap B_1 \) dan \( A \cap B_2 \) juga saling lepas.
Dengan demikian, \( A \cap B_1 \) dan \( A \cap B_2 \) merupakan dua himpunan yang saling lepas, tidak kosong, dan terbuka dalam topologi subruang pada \( A \). Artinya, keduanya membentuk suatu pemisahan dari \( A \).
Hal ini bertentangan dengan asumsi bahwa \( A \) adalah himpunan terhubung.
Oleh karena itu, asumsi tersebut salah, dan kesimpulan yang diinginkan pun terbukti:
$$ A \subset B_1 \quad \text{atau} \quad A \subset B_2 $$
Dengan demikian, bukti selesai.
Dan seterusnya.