Keterhubungan melalui Irisan Tak Kosong

Misalkan \( C_1, C_2, \dots, C_n \subset X \) adalah sekumpulan himpunan terhubung di dalam suatu ruang topologi \( X \), dan anggap bahwa semua himpunan tersebut memiliki setidaknya satu titik yang sama, yaitu: \[
\bigcap_{i=1}^n C_i \neq \varnothing . \] Dalam kondisi ini, gabungan dari semua himpunan tersebut, yakni \( \bigcup_{i=1}^n C_i \), juga merupakan himpunan yang terhubung.

Dengan kata lain, jika dua atau lebih himpunan terhubung memiliki setidaknya satu titik persekutuan, maka gabungannya tetap membentuk satu kesatuan yang terhubung.

Pernyataan ini bergantung secara langsung pada asumsi bahwa irisan semua himpunan tidak kosong.

Catatan. Syarat \( \bigcap_{i=1}^n C_i \neq \varnothing \) cukup untuk menjamin keterhubungan gabungan \( \bigcup_{i=1}^n C_i \), tetapi bukan merupakan syarat yang mutlak. Dalam banyak situasi, gabungan dari himpunan-himpunan terhubung tetap terhubung meskipun tidak ada satu titik pun yang dimiliki bersama oleh semuanya. Hal ini, misalnya, terjadi pada konfigurasi yang melibatkan irisan berantai.

Contoh konkret

Perhatikan himpunan-himpunan berikut di dalam bidang \( \mathbb{R}^2 \):

• \( C_1 \): ruas garis horizontal dari titik \( (-1,0) \) hingga \( (1,0) \)
• \( C_2 \): ruas garis vertikal dari titik \( (0,-1) \) hingga \( (0,1) \)
• \( C_3 \): ruas garis diagonal yang menghubungkan titik \( (-1,-1) \) dan \( (1,1) \)

Ketiga himpunan tersebut masing-masing bersifat terhubung.

Selain itu, semuanya memiliki satu titik yang sama, yaitu:

\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]

Dengan demikian, irisan ketiganya tidak kosong:

\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]

Oleh karena itu, berdasarkan kriteria keterhubungan, gabungan ketiga himpunan tersebut merupakan himpunan yang terhubung:

\[ C_1 \cup C_2 \cup C_3 \]

Ketiga ruas garis tersebut berpotongan pada satu titik pusat yang sama. Inilah yang memastikan bahwa gabungannya tetap terhubung.

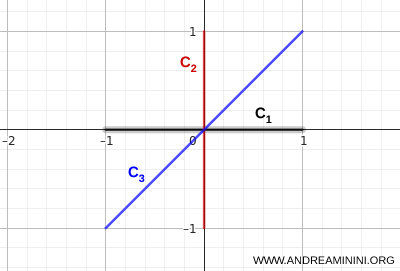
Dari sembarang titik pada salah satu ruas, kita dapat mencapai titik lain dengan bergerak sepenuhnya melalui titik-titik yang termasuk dalam gabungan tersebut.

Catatan. Terdapat pula kriteria keterhubungan lain yang tidak mengharuskan semua himpunan \( C_i \) memiliki satu titik persekutuan. Misalnya, jika himpunan-himpunan tersebut saling beririsan secara berantai, yaitu \( C_i \cap C_{i+1} \neq \varnothing \), maka gabungannya \( \bigcup_i C_i \) tetap terhubung meskipun \( \bigcap_i C_i = \varnothing \). Bahkan, kondisi irisan berantai pun tidak selalu diperlukan. Dalam beberapa kasus, gabungan tetap terhubung meskipun sebagian pasangan himpunan saling terpisah, selama terdapat himpunan lain yang berperan sebagai penghubung. Sebagai contoh, tiga ruas garis yang membentuk sebuah segitiga memiliki irisan total kosong, namun gabungannya tetap terhubung.

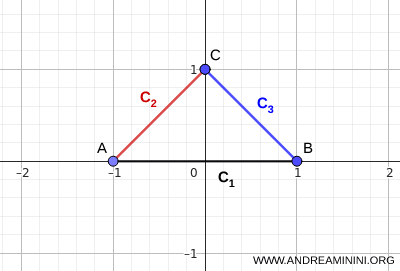
Contoh ini menunjukkan dengan jelas bahwa irisan berantai sudah cukup untuk menjamin keterhubungan gabungan.

Bukti

Misalkan \( X \) adalah suatu ruang topologi dan \( \{C_i\}_{i \in I} \) adalah keluarga himpunan terhubung di dalam \( X \) dengan irisan bersama yang tidak kosong:

\[ \bigcap_{i \in I} C_i \neq \varnothing \]

Andaikan, untuk memperoleh kontradiksi, bahwa gabungan

\[ C = \bigcup_{i \in I} C_i \]

tidak terhubung.

Jika \( C \) tidak terhubung, maka terdapat dua himpunan terbuka \( U \) dan \( V \) yang membentuk suatu pemisahan dari \( C \), yaitu:

• \( U \cap C \neq \varnothing \)
• \( V \cap C \neq \varnothing \)
• \( (U \cap C) \cap (V \cap C) = \varnothing \)
• \( C = (U \cap C) \cup (V \cap C) \)

Karena irisan semua himpunan \( C_i \) tidak kosong, terdapat suatu titik \( x \in C \) yang termasuk ke dalam setiap \( C_i \):

\[ x \in \bigcap_{i \in I} C_i \]

Titik ini harus berada di salah satu dari \( U \) atau \( V \), tetapi tidak mungkin berada pada keduanya sekaligus, karena keduanya membentuk pemisahan dari \( C \). Misalkan, tanpa mengurangi keumuman, bahwa

\[ x \in U \quad \text{dan} \quad x \notin V \]

Karena setiap \( C_i \subset C \), kita dapat menuliskan:

\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]

Karena \( C_i \cap U \) dan \( C_i \cap V \) terbuka dalam topologi relatif pada \( C_i \), saling terpisah, dan secara bersama-sama menutupi \( C_i \), serta karena setiap \( C_i \) bersifat terhubung, maka salah satu dari kedua himpunan tersebut harus kosong.

Dengan demikian, setiap \( C_i \) seluruhnya berada di dalam salah satu dari \( U \) atau \( V \):

\[ C_i \subset U \quad \text{atau} \quad C_i \subset V \]

Karena \( x \in C_i \) dan \( x \in U \), maka tidak mungkin berlaku bahwa \( C_i \subset V \).

Akibatnya:

\[ C_i \subset U \quad \text{untuk setiap } i \in I \]

Dengan demikian, gabungan \( C \) merupakan bagian dari \( U \):

\[ \bigcup_{i \in I} C_i \subset U \]

Hal ini bertentangan dengan asumsi bahwa \( V \cap C \neq \varnothing \).

Kontradiksi ini menunjukkan bahwa asumsi awal keliru. Oleh karena itu, gabungan \( \bigcup_{i \in I} C_i \) merupakan himpunan yang terhubung.

Dan seterusnya.