Pemisahan Subhimpunan oleh Himpunan Terbuka

Misalkan $ A $ adalah sebuah subhimpunan dalam ruang topologi $ X $. Dua himpunan terbuka $ U $ dan $ V $ dikatakan membentuk pemisahan bagi $ A $ apabila ketiga syarat berikut terpenuhi:

Mereka menutupi seluruh $ A $ \[ A \subseteq U \cup V \]
Masing-masing beririsan dengan $ A $ dalam himpunan yang tidak kosong \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
Mereka saling lepas ketika dibatasi pada $ A $ \[ U \cap V \cap A = \varnothing \]

Dengan kata lain, $ A $ terbagi menjadi dua bagian yang tidak saling menyentuh. Satu bagian seluruhnya berada di dalam $ U $, sementara bagian lainnya berada di dalam $ V $. Tidak ada bagian dari $ A $ yang berada dalam irisan kedua himpunan tersebut.

Konsep ini merupakan salah satu cara paling jelas dalam topologi untuk menyatakan bahwa sebuah subhimpunan benar-benar terpisah secara struktural.

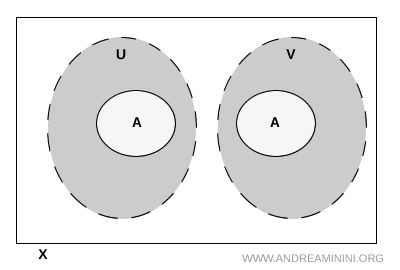
diagram yang menggambarkan pemisahan subhimpunan oleh himpunan terbuka

Nota. Penting untuk ditekankan bahwa $ U $ dan $ V $ tidak harus saling lepas di seluruh ruang $ X $. Mereka mungkin saja beririsan di luar $ A $. Yang menentukan adalah bahwa irisan tersebut tidak menyentuh bagian mana pun dari $ A $.
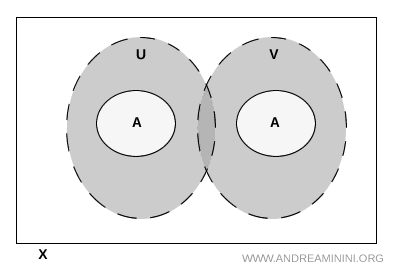
diagram yang menunjukkan bahwa U dan V dapat beririsan di luar subhimpunan A

Contoh

Untuk melihat gagasan ini secara konkret, perhatikan ruang topologi $ X = \mathbb{R} $ dengan topologi standar. Misalkan kita mengambil:

$$ A = [-2,-1] \cup [1,2] $$

Dua interval ini terpisah secara jelas. Sekarang definisikan dua himpunan terbuka berikut:

$$ U = (-3,0) $$

$$ V = (0,3) $$

Jika kita gambarkan, situasinya tampak seperti berikut:

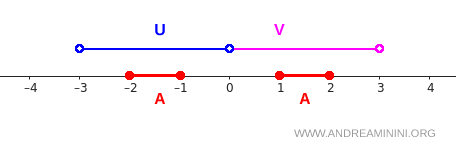
grafik himpunan terbuka U dan V beserta subhimpunan A

Interval $ [-2,-1] $ seluruhnya berada di dalam $ U $. Interval $ [1,2] $ seluruhnya berada di dalam $ V $. Kondisi pertama pemisahan langsung terpenuhi, karena:

$$ A \subseteq U \cup V $$

Kondisi kedua juga terpenuhi, sebab masing-masing himpunan terbuka benar-benar beririsan dengan bagian tertentu dari $ A $:

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

Terakhir, tidak ada titik di mana $ U $ dan $ V $ bersinggungan di dalam $ A $:

$$ U \cap V \cap A = \varnothing $$

Ketiga syarat ini menunjukkan bahwa $ U $ dan $ V $ membentuk pemisahan yang sah bagi subhimpunan $ A $ di dalam ruang topologi $ X $. Tinjauan semacam ini sering muncul dalam pembahasan mengenai keterhubungan, pemetaan kontinu, dan struktur ruang secara umum.