نظرية: توصيف الفضاءات المتصلة من خلال المجموعات المفتوحة والمغلقة

يُقال إن الفضاء الطوبولوجي \( X \) هو متصل إذا وفقط إذا كانت المجموعات الجزئية الوحيدة من \( X \) التي تُعد في الوقت نفسه مفتوحة ومغلقة (المعروفة باسم كلوبن) هي الفضاء نفسه \( X \) والمجموعة الخالية \( \emptyset \).

بمعنى آخر، يكون الفضاء متصلًا عندما لا يمكن تقسيمه إلى مجموعتين مفتوحتين، منفصلتين وغير فارغتين. في هذه الحالة، المجموعات الكلوبن الوحيدة الممكنة هي الفضاء الكامل والمجموعة الخالية.

هذا التعريف يُقدّم معيارًا بسيطًا وفعّالًا لفهم الاتصال الطوبولوجي. فهو يتيح التحقق من كون الفضاء متصلًا دون الحاجة إلى استخدام مفاهيم أكثر تقدمًا مثل الاتصال بالمسارات.

الفكرة الأساسية

في الطوبولوجيا، عندما تكون مجموعة ما مفتوحة ومغلقة في الوقت نفسه، فإنها تُحدث فصلًا داخل الفضاء. أي أنها تُجزّئ \( X \) إلى مجموعتين مفتوحتين، منفصلتين وغير فارغتين.

إذا وُجدت مثل هذه المجموعة، فهذا يعني أن الفضاء يمكن تمثيله باتحاد مجموعتين مفتوحتين ومنفصلتين، أي أنه غير متصل. أما إذا كانت المجموعات الكلوبن الوحيدة هي \( X \) و\( \emptyset \)، فذلك يعني أن الفضاء متصل ولا يمكن فصله طوبولوجيًا.

ملاحظة: في أي فضاء طوبولوجي، تكون المجموعة الكلية \( X \) والمجموعة الخالية \( \emptyset \) دائمًا مفتوحتين ومغلقتين معًا. وهما المثالان البسيطان للمجموعات الكلوبن.

مثال 1: فضاء منتهٍ غير متصل

لنأخذ \( X = \{ a, b, c, d \} \) مع الطوبولوجيا \( T \) المحددة بالمجموعات المفتوحة: \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \).

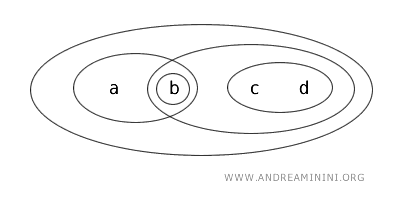
في هذا الفضاء، المجموعة \( \{ a, b \} \) هي كلوبن لأنها:

• مفتوحة، لأنها ضمن عائلة المجموعات المفتوحة في \( T \)؛
• ومغلقة، لأن متممتها \( \{ c, d \} \) مفتوحة أيضًا في \( T \).

بما أن \( (X, T) \) يحتوي على مجموعة غير خالية وصحيحة (أي ليست الفضاء كله) وهي كلوبن، نستنتج أنه غير متصل.

يكفي وجود مجموعة كلوبن واحدة غير تافهة لإثبات أن الفضاء غير متصل، لأن ذلك يعني أنه يمكن كتابته كاتحاد مجموعتين مفتوحتين منفصلتين وغير فارغتين: \( \{ a, b \} \) و\( \{ c, d \} \). في هذه الحالة، لا يتحقق شرط الاتصال الطوبولوجي.

مثال 2: المستقيم الحقيقي

لننظر إلى مجموعة الأعداد الحقيقية \( \mathbb{R} \) المزودة بـالطوبولوجيا الاعتيادية الناتجة عن الفواصل المفتوحة \( (a, b) \).

في هذه الطوبولوجيا، تكون الفواصل \( (a, b) \) مفتوحة لكنها ليست مغلقة، بينما الفواصل \( [a, b] \) مغلقة لكنها ليست مفتوحة.

إذن، المجموعات الوحيدة في \( \mathbb{R} \) التي تُعد مفتوحة ومغلقة معًا هي \( \mathbb{R} \) و\( \emptyset \). وهذا يعني أن المستقيم الحقيقي فضاء متصل.

مثال 3: فضاء جزئي غير متصل من \( \mathbb{R} \)

لنأخذ الفضاء الجزئي \( X = (0,1) \cup (2,3) \subset \mathbb{R} \) المزود بـالطوبولوجيا الفرعية المستمدة من الطوبولوجيا الاعتيادية على \( \mathbb{R} \).

في هذا الفضاء، الفاصلتان \( (0,1) \) و\( (2,3) \) مفتوحتان ومغلقتان في الوقت نفسه داخل \( X \)، لأن متممة كل منهما في \( X \) هي الأخرى. وبالتفصيل:

• متممة \( (0,1) \) في \( X \) هي \( (2,3) \)، وهي مفتوحة في \( X \)؛
• ومتممة \( (2,3) \) في \( X \) هي \( (0,1) \)، وهي أيضًا مفتوحة في \( X \).

هاتان المجموعتان إذن كلوبن، مما يعني أن الفضاء \( X \) غير متصل.

أي أن \( X \) يتكوّن من مركبتين متصلتين منفصلتين هما \( (0,1) \) و\( (2,3) \). كل منهما مفتوحة وغير فارغة، ولا يمكن ربط نقطة من الأولى بأخرى من الثانية بواسطة دالة مستمرة. وهذه بالضبط هي خاصية عدم الاتصال في الطوبولوجيا.