توصيف عدم اتصال المجموعات بواسطة المجموعات المفتوحة في الفضاءات الطوبولوجية

هذا التوصيف يوفر طريقة مباشرة وسهلة للتحقق من عدم الاتصال. إذا استطعت العثور على مجموعتين مفتوحتين تفصلان \(A\)، فقد حسمت المسألة فوراً.

لماذا يعد هذا التوصيف مفيداً؟

لأن الطوبولوجيا لا تعتمد على المسافة، بل على البنية المفتوحة للفضاء. لذلك، ربط الاتصال بالمجموعات المفتوحة يجعل المفهوم عاماً، مرناً، وينطبق على فضاءات معقدة تتجاوز الهندسة المألوفة.

مثال توضيحي

لنبدأ بحالة بسيطة جداً على خط الأعداد الحقيقي \(\mathbb{R}\):

$$ A = [0,1] \cup [2,3] $$

هذه المجموعة غير متصلة بوضوح، فهي تتكون من مقطعين منفصلين تماماً. وطبقاً للتوصيف، لا بد من وجود مجموعتين مفتوحتين تفصلان الجزأين عن بعضهما.

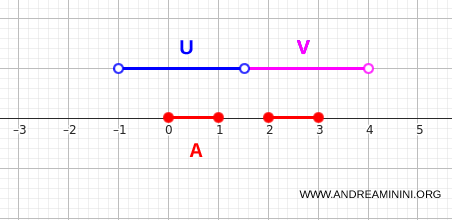
يمكن اختيار:

• $ U = (-1,1.5) $
• $ V = (1.5,4) $

كل منهما يغطي جزءاً من \(A\) دون أن يلتقيا على أي نقطة منه، وهو ما يوضح تماماً سبب عدم الاتصال:

$$ U \cap A = [0,1] $$

$$ V \cap A = [2,3] $$

$$ (U \cap V) \cap A = \varnothing $$

مثال آخر

لننتقل إلى مجموعة أبسط:

$$ A = \{1, 3\} $$

بما أن النقاط منفصلة ولا يوجد مسار يربط بينهما داخل المجموعة، فهي أيضاً غير متصلة. ويمكن التأكد باستخدام مجموعات مفتوحة تفصل العنصرين:

$$ U = (0,2), \quad V = (2,4) $$

كل مجموعة تحتوي نقطة واحدة فقط، ولا يوجد بينهما أي تقاطع داخل \(A\):

$$ U \cap A = \{1\}, \quad V \cap A = \{3\} $$

$$ U \cap V \cap A = \varnothing $$

هكذا نحصل على فصل واضح للمجموعة.

مثال في بعد أعلى

لننظر الآن في فضاء ثنائي الأبعاد بعد حذف المحور \(x\):

$$ A = \{(x,y)\in\mathbb{R}^2: y>0\} \cup \{(x,y)\in\mathbb{R}^2: y<0\} $$

النصف الأعلى والنصف الأسفل من المستوي لا يتصلان ببعضهما عند غياب المحور. يمكن استخدام مجموعتين مفتوحتين تغطيان كل نصف دون تقاطع في \(A\):

$$ U = \{(x,y): y>-1\} $$

$$ V = \{(x,y): y<1\} $$

النصفان يبقيان منفصلين تماماً:

$$ (U \cap V) \cap A = \varnothing $$

البرهان بإيجاز

يعتمد البرهان على فكرتين بسيطتين:

1. إذا وُجدت مجموعات مفتوحة تفصل \(A\)، فهي غير متصلة

يكفي أخذ:

$$ P = U \cap A, \quad Q = V \cap A $$

ستكون \(P\) و\(Q\) مجموعتين منفصلتين، مفتوحتين في الطوبولوجيا الجزئية، وغير فارغتين، وتشكلان معاً المجموعة \(A\). وهذا بالضبط تعريف عدم الاتصال.

2. إذا كانت \(A\) غير متصلة، يمكن دائماً إيجاد مثل هذه المجموعات المفتوحة

فكل فصل في \(A\) يمكن تمديده إلى مجموعتين مفتوحتين في \(X\) تغطيان \(A\) وتفصلان بين جزأيها.

الخلاصة

عدم الاتصال ليس مفهوماً مجرداً أو غامضاً. يمكن فهمه بوضوح من خلال المجموعات المفتوحة: إذا تمكنت من تغطية مجموعة جزئية \(A\) بمجموعتين مفتوحتين متباينتين تلتقط كل منهما جزءاً مختلفاً من \(A\)، فقد أثبتَّ أنها غير متصلة.

هذا التوصيف يجعل التعامل مع الاتصال وعدم الاتصال أكثر سهولة ووضوحاً، خاصة في الفضاءات التي يصعب تصورها هندسياً.