ما هو الفضاء المتصل في الطوبولوجيا؟
التعريف من خلال المجموعات المفتوحة
يُقال إن الفضاء الطوبولوجي $ X $ هو متصل إذا لم يمكن تقسيمه إلى مجموعتين مفتوحتين غير فارغتين ومتباينتين $ U $ و$ V $ يكون اتحادهما هو الفضاء بأكمله $ X $.
- $ U \neq \emptyset $ و$ V \neq \emptyset $ - كلتاهما غير فارغتين؛
- $ U \cap V = \emptyset $ - لا تتقاطعان إطلاقًا؛
- $ U \cup V \ne X $ - اتحادهما لا يغطي الفضاء بالكامل.
إذا وُجد مثل هذا الزوج من المجموعات، فإن الفضاء يُسمّى منفصلًا.
بكلمات أبسط، الفضاء يكون متصلًا عندما لا يمكن تقسيمه إلى منطقتين مفتوحتين مستقلتين. وإذا أمكن فعل ذلك، فهو منفصل، ويُسمّى الزوج (U, V) فصلًا للفضاء (X).
ملاحظة. هذا هو تعريف الاتصال الطوبولوجي بالاعتماد على المجموعات المفتوحة. وكما سنرى، يختلف هذا المفهوم عن الاتصال بالمسار أو الاتصال بالقوس، وهما ليسا متكافئين دائمًا.
مثال توضيحي
لنفترض أن لدينا مجموعة بسيطة مكوّنة من ثلاثة عناصر:
$$ X = {a, b, c} $$
وسنضع عليها طوبولوجيتين مختلفتين:
- الطوبولوجيا A
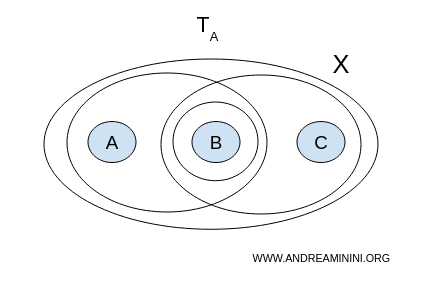
المجموعات المفتوحة فيها هي: $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$ - الطوبولوجيا B
أما هنا فالمجموعات المفتوحة هي: $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$
الآن، أيّ الفضاءين متصل؟
1. الطوبولوجيا A
نبحث عن فصل (U, V)، أي عن مجموعتين مفتوحتين غير فارغتين ومتباينتين يكون اتحادهما $ X $ بأكمله.
- $ U = {a,b}, V = {b,c} $ ليستا متباينتين لأنهما تحتويان على $ b $؛
- $ U = {a,b}, V = {b} $ ليستا متباينتين؛
- $ U = {b}, V = {b,c} $ ليستا متباينتين.
لا يوجد أي زوج من المجموعات المفتوحة يحقق شروط الانفصال، لذا فإن الفضاء $ X $ مع الطوبولوجيا A هو متصل.
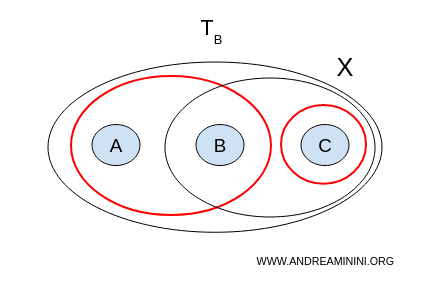
2. الطوبولوجيا B
نبحث الآن عن فصل (U, V) في الطوبولوجيا B:
- $ U = {a,b}, V = {b,c} $ ليستا متباينتين لأنهما تشتركان في العنصر $ b $؛
- $ U = {a,b}, V = {c} $ مجموعتان مفتوحتان غير فارغتين ومتباينتان، واتحادهما يغطي الفضاء بأكمله: $ U \cup V = {a,b,c} = X $.
إذن الفضاء $ X $ المزود بالطوبولوجيا B هو منفصل.
ملاحظة. نلاحظ هنا أن خاصية الاتصال لا تعتمد على العناصر نفسها، بل على نوع الطوبولوجيا المفروضة عليها. فالمجموعة واحدة، لكن الطوبولوجيا تغيّر طبيعة الفضاء بالكامل.
مثال آخر: خط الأعداد الحقيقية بدون نقطة
لنفترض أن لدينا الفضاء:
$$ X = (-\infty, n) \cup (n, +\infty) $$
أي خط الأعداد الحقيقية بعد إزالة النقطة $ n $ منه:
$$ X = \mathbb{R} \setminus {n} $$
هل هذا الفضاء متصل؟
لنأخذ:
- $ U = (-\infty, n) $
- $ V = (n, +\infty) $
هاتان المجموعتان مفتوحتان، متباينتان، غير فارغتين، واتحادهما هو $ X $. وهذا يحقق شروط الفصل تمامًا.
إذًا، الفضاء $ X $ منفصل.
ملاحظة. حذف نقطة واحدة من خط الأعداد يجعل الخط “ينكسر”. يصبح لدينا جزآن منفصلان - أحدهما على يسار $ n $ والآخر على يمينه - ولا يمكن وصلهما بمسار مستمر. لذلك، الفضاء هنا منفصل وغير متصل بالمسار.
الفرق بين الاتصال الطوبولوجي والاتصال بالمسار
من المهم أن نميّز بين هذين المفهومين:
- الاتصال الطوبولوجي: لا يمكن تقسيم الفضاء إلى مجموعتين مفتوحتين غير فارغتين ومتباينتين يغطي اتحادهما الفضاء بأكمله.
- الاتصال بالمسار: يمكن ربط أي نقطتين في الفضاء بمسار مستمر يقع بالكامل داخله. وإذا لم يمر المسار بالنقطة نفسها مرتين، يُقال إن الفضاء متصل بالقوس.
كل فضاء متصل بالمسار هو بالضرورة متصل طوبولوجيًا، لكن العكس ليس صحيحًا دائمًا.
وجود مسار مستمر بين نقطتين يمنع تقسيم الفضاء إلى منطقتين منفصلتين. غير أن بعض الفضاءات متصلة طوبولوجيًا لكنها تفتقر إلى الاتصال بالمسار.
مثال كلاسيكي: منحنى الجيب للرياضيين: $$ S = { (x, \sin(1/x)) \mid x > 0 } \cup { (0, y) \mid -1 \le y \le 1 } $$
هذا الفضاء متصل لأنه لا يمكن فصله إلى مجموعتين مفتوحتين، لكنه غير متصل بالمسار، إذ لا يمكن رسم مسار مستمر يصل بين نقطة على الجزء المتموّج وأخرى على المقطع العمودي.
هكذا نرى كيف يمكن لخاصية الاتصال أن تكشف عن البنية العميقة للفضاء الطوبولوجي.
ملاحظات
ملاحظات إضافية حول الفضاءات المتصلة
- نظرية: توصيف الفضاءات المتصلة باستخدام المجموعات المفتوحة والمغلقة (كلوبن)
يكون الفضاء الطوبولوجي \( X \) متصلًا إذا وفقط إذا كانت المجموعات الجزئية الوحيدة من \( X \) التي تُعد في آنٍ واحد مفتوحة ومغلقة (كلوبن) هي الفضاء نفسه \( X \) والمجموعة الخالية \( \emptyset \).
وهكذا تُستكمل الملاحظات المتعلقة بخصائص الاتصال الطوبولوجي.