فصل مجموعة فرعية باستخدام مجموعات مفتوحة

إذا كانت لدينا مجموعة فرعية $ A $ داخل فضاء طوبولوجي $ X $، فيمكن أحياناً تقسيم هذه المجموعة إلى جزأين منفصلين باستخدام مجموعات مفتوحة. يحدث ذلك عندما توجد مجموعتان مفتوحتان $ U $ و$ V $ تحققان شروطاً واضحة وبسيطة:

أن تغطيا المجموعة $ A $ بالكامل \[ A \subseteq U \cup V \]
أن يلتقي كل منهما مع $ A $ في جزء غير فارغ \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
ألا تتقاطعان فوق $ A $ إطلاقاً \[ U \cap V \cap A = \varnothing \]

بهذه الشروط ينقسم $ A $ إلى جزأين منفصلين: جزء يقع داخل $ U $ وجزء آخر داخل $ V $. وهذا هو الأسلوب الطوبولوجي القياسي للتعبير عن أن مجموعة ما مفصولة إلى مكوّنين لا يتداخلان.

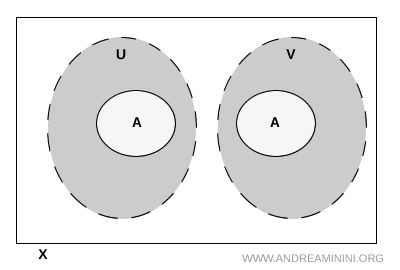
رسم يوضح فصل مجموعة فرعية باستخدام مجموعات مفتوحة

ملاحظة. ليس من الضروري أن تكون المجموعتان $ U $ و$ V $ منفصلتين في الفضاء كله. قد تلتقيان خارجه، وهذا لا يسبب أي مشكلة. المهم هو ألا يلامس تقاطعهما المجموعة $ A $.
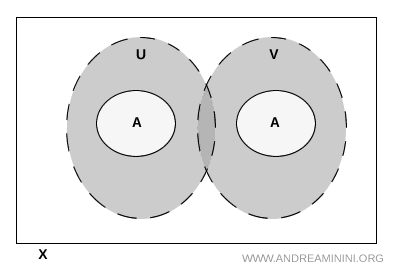
رسم يوضح إمكانية تقاطع U و V خارج المجموعة الفرعية A

مثال يوضح الفكرة

لنجعل الفكرة أكثر وضوحاً من خلال مثال بسيط. نأخذ الفضاء $ X = \mathbb{R} $ مع الطوبولوجيا المعيارية، ونفترض أن:

$$ A = [-2,-1] \cup [1,2] $$

أي أن $ A $ مكوّنة من مقطعين مغلقين منفصلين. ونعرّف مجموعتين مفتوحتين في $ X $:

$$ U = (-3,0) $$

$$ V = (0,3) $$

هكذا يبدو الشكل:

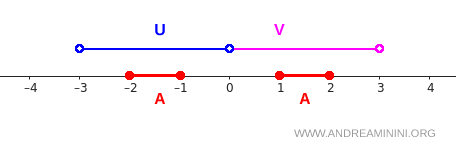
رسم يوضح المجموعتين المفتوحتين U و V مع المجموعة الفرعية A

من الواضح أن المقطع $ [-2,-1] $ يقع بالكامل داخل $ U $، بينما المقطع $ [1,2] $ يقع بالكامل داخل $ V $. بهذا نضمن أن:

$$ A \subseteq U \cup V $$

وأن كلا المجموعتين المفتوحتين تلتقيان مع $ A $ في جزء غير فارغ:

$$ U \cap A = [-2,-1] $$

$$ V \cap A = [1,2] $$

كما لا يوجد أي تقاطع بين $ U $ و$ V $ على $ A $:

$$ U \cap V \cap A = \varnothing $$

بهذا نكون قد تحققنا من أن $ U $ و$ V $ تفصلان فعلاً المجموعة $ A $ داخل الفضاء $ X $. هذه الطريقة البسيطة والمباشرة تُعد من الأدوات الأساسية في دراسة الفضاءات غير المتصلة والخصائص الطوبولوجية المرتبطة بها.