كل مجموعة متصلة محتواة داخل مكوّن متصل واحد

لتكن \( A \) و\( B \) مجموعتين جزئيتين من فضاء طوبولوجي \( X \)، حيث إن \( A \) مجموعة متصلة وتحقق \( A \subset B \). إذا أمكن فصل المجموعة \( B \) طوبولوجيا إلى مجموعتين جزئيتين \( B_1 \) و\( B_2 \) داخل الفضاء \( X \)، فإن المجموعة المتصلة \( A \) لا يمكن إلا أن تكون محتواة بالكامل في إحدى هاتين المجموعتين، أي: $$ A \subset B_1 \quad \text{أو} \quad A \subset B_2 $$

الفكرة الأساسية بسيطة ومهمة في آن واحد: لا تستطيع أي مجموعة متصلة أن تمتد عبر طرفي فصل طوبولوجي في الوقت نفسه.

بعبارة أخرى، إذا كانت مجموعة متصلة موجودة داخل مجموعة أكبر يمكن تقسيمها إلى جزأين منفصلين، فلا بد أن تقع هذه المجموعة المتصلة بكاملها داخل أحد الجزأين دون الآخر.

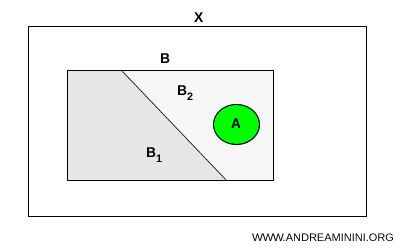
للتقريب الحدسي، يمكن تصور المجموعة المتصلة على أنها قطعة حبل واحدة غير مقطوعة موضوعة داخل ظرف. فإذا قُسِّم الظرف إلى حجرتين منفصلتين وبقي الحبل سليما، فلا بد أن يوجد الحبل كله داخل إحدى الحجرتين. أما وجوده في كلتيهما فيتطلب قطعه. بهذا المعنى، تمنع خاصية الاتصال أي مجموعة من الامتداد عبر فصل طوبولوجي، تماما كما يستحيل تقسيم حبل سليم دون كسره.

مثال توضيحي

لنأخذ الفضاء الطوبولوجي التالي:

$$ X = \mathbb{R} $$

وننظر في المجموعة الجزئية:

$$ B = (-3,4) $$

يمكن فصل هذه المجموعة إلى مجموعتين جزئيتين كما يلي:

$$ B_1 = (-3,0) $$

$$ B_2 = (0,4) $$

هاتان المجموعتان متباينتان تماما، إذ:

$$ B_1 \cap B_2 = \varnothing $$

وفي الوقت نفسه، فإن اتحادهما يعيد المجموعة الأصلية \( B \):

$$ B_1 \cup B_2 = B $$

كما أن كلا من \( B_1 \) و\( B_2 \) مجموعة مفتوحة في طوبولوجيا الفضاء الجزئي المعرفة على \( B \)، ولهذا فهما تشكلان فصلا طوبولوجيا حقيقيا للمجموعة \( B \).

الآن، لننظر في مجموعة جزئية متصلة من \( B \):

$$ A = (1,2) $$

نلاحظ مباشرة أن \( A \subset B_2 \)، أي إن المجموعة \( A \) تقع بالكامل داخل أحد جزئي الفصل، كما تنص القاعدة العامة.

ملاحظة. لو حاولنا اختيار \( A = (-1,1) \)، فسنجد أن $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ لكن هذا الوضع غير ممكن، لأن \( B_1 \) و\( B_2 \) يشكلان فصلا طوبولوجيا للمجموعة \( B \). فالمجموعة الجزئية المتصلة لا يمكن أن تتوزع على جزئي فصل واحد. ولو كان ذلك ممكنا، لكانت \( A \) نفسها قابلة للفصل، وهو ما يناقض حقيقة أن الفترة \( (-1,1) \) مجموعة متصلة. المشكلة ليست في فقدان الاتصال، بل في استحالة احتواء \( A \) داخل \( B \) عندما تكون \( B \) مفصولة بهذه الطريقة.

البرهان

الفرضيات

لتكن \( A \) و\( B \) مجموعتين جزئيتين من فضاء طوبولوجي \( X \)، بحيث:

$$ A \subset X \quad \text{و} \quad B \subset X $$

ونفترض ما يلي:

• \( A \) مجموعة متصلة
• \( A \subset B \)
• \( B_1 \) و\( B_2 \) يشكلان فصلا طوبولوجيا للمجموعة \( B \) في \( X \)

النتيجة

نريد أن نبرهن أن:

$$ A \subset B_1 \quad \text{أو} \quad A \subset B_2 $$

البرهان

بما أن \( B_1 \) و\( B_2 \) يشكلان فصلا طوبولوجيا للمجموعة \( B \)، فإن:

• \( B_1 \cap B_2 = \varnothing \)
• \( B = B_1 \cup B_2 \)
• \( B_1 \) و\( B_2 \) مفتوحتان في طوبولوجيا الفضاء الجزئي على \( B \)

نفترض جدلا أن \( A \) ليست محتواة بالكامل في أي من \( B_1 \) أو \( B_2 \). عندئذ:

$$ A \cap B_1 \neq \varnothing \qquad \text{و} \qquad A \cap B_2 \neq \varnothing $$

وبما أن \( A \subset B \)، يمكن كتابة:

$$ A = (A \cap B_1) \cup (A \cap B_2) $$

وتكون المجموعتان \( A \cap B_1 \) و\( A \cap B_2 \) متباينتين، غير فارغتين، ومفتوحتين في طوبولوجيا الفضاء الجزئي على \( A \).

وهذا يعني أن \( A \) نفسها تقبل فصلا طوبولوجيا، وهو ما يناقض فرضية اتصالها.

وعليه، لا بد أن يكون أحد الاحتمالين صحيحا:

$$ A \subset B_1 \quad \text{أو} \quad A \subset B_2 $$

وبهذا يكتمل البرهان.