الاتصال بوجود تقاطع مشترك
لتكن \( C_1, C_2, \dots, C_n \subset X \) عائلة من المجموعات المتصلة داخل فضاء طوبولوجي \( X \)، بحيث تشترك جميعها في نقطة واحدة على الأقل، أي:
\[ \bigcap_{i=1}^n C_i \neq \varnothing . \]
في هذه الحالة يكون اتحادها \( \bigcup_{i=1}^n C_i \) مجموعة متصلة.
بعبارة أبسط، إذا اشتركت مجموعتان متصلتان أو أكثر في نقطة واحدة على الأقل، فإن اتحادها يبقى متصلاً.
يعتمد هذا المبدأ على افتراض أساسي مفاده أن جميع المجموعات تتقاطع في نقطة مشتركة.
ملاحظة. إن الشرط \( \bigcap_{i=1}^n C_i \neq \varnothing \) شرط كافٍ لضمان اتصال الاتحاد، لكنه ليس شرطاً ضرورياً. فقد يكون اتحاد مجموعات متصلة متصلاً حتى في غياب نقطة مشتركة بينها جميعاً، كما يحدث مثلاً عندما تكون المجموعات مترابطة على نحوٍ تسلسلي.
مثال توضيحي
لننظر في المجموعات التالية ضمن الفضاء \( \mathbb{R}^2 \):
- \( C_1 \): القطعة الأفقية الممتدة من \( (-1,0) \) إلى \( (1,0) \)
- \( C_2 \): القطعة العمودية الممتدة من \( (0,-1) \) إلى \( (0,1) \)
- \( C_3 \): القطعة القطرية الواصلة بين \( (-1,-1) \) و \( (1,1) \)
كل واحدة من هذه المجموعات متصلة.
كما أنها جميعاً تحتوي على النقطة \( (0,0) \)، أي:
\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]
ومن ثم فإن التقاطع المشترك غير فارغ:
\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]
وبناءً على معيار الاتصال، يكون اتحاد هذه المجموعات متصلاً:
\[ C_1 \cup C_2 \cup C_3 \]
تلتقي القطع الثلاث في نقطة مركزية واحدة، وهذا يكفي لضمان اتصال الاتحاد.
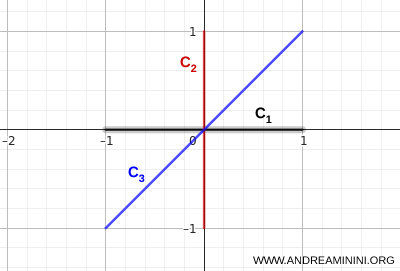
ومن أي نقطة على إحدى هذه القطع، يمكن الوصول إلى أي نقطة أخرى عبر مسار يتكوّن بالكامل من نقاط تنتمي إلى هذا الاتحاد.
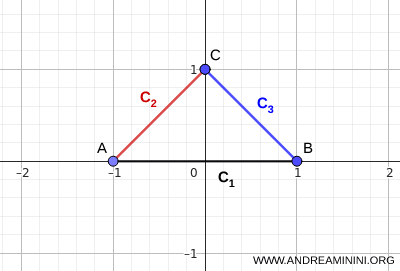
ملاحظة. توجد معايير أخرى للاتصال لا تشترط وجود نقطة مشتركة بين جميع المجموعات \( C_i \). فعلى سبيل المثال، إذا كانت هذه المجموعات متصلة وتتقاطع على نحوٍ تسلسلي، أي إذا تحقق \( C_i \cap C_{i+1} \neq \varnothing \)، فإن اتحادها \( \bigcup_i C_i \) يكون متصلاً حتى في حال كان \( \bigcap_i C_i = \varnothing \). ومع ذلك، فإن هذا الشرط ليس ضرورياً أيضاً، إذ قد يبقى الاتحاد متصلاً حتى عندما تكون بعض الأزواج المتتالية منفصلة، ما دامت مجموعات أخرى تؤدي دور الوسيط بينها. فعلى سبيل المثال، إذا شكّلت ثلاث قطع مثلثاً، فإن تقاطعها الكلي يكون فارغاً، أي \( \bigcap_i C_i = \varnothing \)، ومع ذلك يبقى الاتحاد متصلاً.
البرهان
ليكن \( X \) فضاءً طوبولوجياً، ولتكن \( \{C_i\}_{i \in I} \) عائلة من المجموعات المتصلة في \( X \) ذات تقاطع مشترك غير فارغ:
\[ \bigcap_{i \in I} C_i \neq \varnothing \]
نفترض، بغرض البرهان بالخلف، أن الاتحاد
\[ C = \bigcup_{i \in I} C_i \]
غير متصل.
عندئذٍ توجد مجموعتان مفتوحتان \( U \) و \( V \) تشكلان فصلاً لـ \( C \)، أي:
- \( U \cap C \neq \varnothing \)
- \( V \cap C \neq \varnothing \)
- \( (U \cap C) \cap (V \cap C) = \varnothing \)
- \( C = (U \cap C) \cup (V \cap C) \)
وبما أن تقاطع المجموعات \( C_i \) غير فارغ، فهناك عنصر \( x \in C \) ينتمي إلى جميع هذه المجموعات:
\[ x \in \bigcap_{i \in I} C_i \]
ولا بد أن ينتمي هذا العنصر إما إلى \( U \) أو إلى \( V \)، ولكن ليس إليهما معاً، لأنهما يشكلان فصلاً لـ \( C \). ولنفرض، دون فقدان للعمومية، أن:
\[ x \in U \quad \text{و} \quad x \notin V \]
وبما أن كل مجموعة \( C_i \subset C \)، يمكن كتابة:
\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]
وبما أن المجموعتين \( C_i \cap U \) و \( C_i \cap V \) مفتوحتان في الطوبولوجيا الجزئية على \( C_i \)، ومتباينتان، وتغطيان \( C_i \) معاً، وبما أن كل \( C_i \) متصلة، فلا بد أن تكون إحدى المجموعتين فارغة.
وعليه، فإن كل مجموعة \( C_i \) تقع بالكامل إما داخل \( U \) أو داخل \( V \):
\[ C_i \subset U \quad \text{أو} \quad C_i \subset V \]
وبما أن \( x \in C_i \) و \( x \in U \)، فلا يمكن أن تكون \( C_i \subset V \).
ومن ثم نحصل على:
\[ C_i \subset U \quad \text{لكل } i \in I \]
وبالتالي فإن الاتحاد \( C \) محتوى في \( U \):
\[ \bigcup_{i \in I} C_i \subset U \]
وهذا يناقض الفرض القائل بأن \( V \cap C \neq \varnothing \).
ومن ثم يتبين أن الافتراض الأولي غير صحيح، وبالتالي فإن الاتحاد \( \bigcup_{i \in I} C_i \) مجموعة متصلة.
وهكذا.