定理：用开闭集理解连通空间

拓扑空间 \( X \) 被称为连通的，当且仅当它唯一同时既开又闭的子集（即 开闭集 或 clopen 集）只有整个空间 \( X \) 和空集 \( \emptyset \)。

简单来说，一个空间连通，意味着它无法被划分成两个互不相交、彼此独立的开子集。

换句话说，一个拓扑空间连通的充要条件是：它唯一的开闭集只有两个 - - 整个空间和空集。

这一判据是判断空间是否连通的一个直观而重要的方法。

为什么会这样？

在拓扑学中，如果某个子集既是开集又是闭集，就意味着这个子集可以把空间分成两个互不相交的非空开集。

当这样的“非平凡”开闭集存在时（即它既不是 \( X \)，也不是 \( \emptyset \)），空间就被分割开了，这样的空间就是非连通的。

反之，如果一个空间的开闭集只有 \( X \) 和 \( \emptyset \)，那它无法被这样分割，因此是连通空间。

提示：无论什么拓扑空间，整个集合 \( X \) 和空集 \( \emptyset \) 总是既开又闭的。

设 \( X = \{ a, b, c, d \} \)，其拓扑 \( T \) 定义如下：开集为 \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \)。

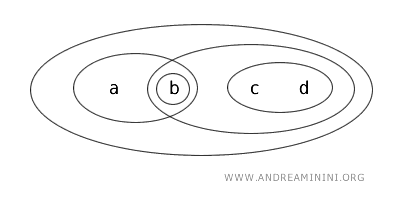
离散拓扑中开闭子集示意图

在这个拓扑中，子集 \( \{ a, b \} \) 同时是开集和闭集：

因此，拓扑空间 \( (X, T) \) 是非连通的。只要存在这样一个非平凡的开闭子集，就足以说明空间不连通。

换个角度看，空间 \( X \) 可以分成两个互不相交的非空开集 \( \{ a, b \} \) 与 \( \{ c, d \} \)，因此它不具备拓扑连通性。

考虑实数集 \( \mathbb{R} \)，赋予其标准拓扑，也就是由开区间 \( (a, b) \) 生成的拓扑。

在这种拓扑下，区间 \( (a, b) \) 是开集但不是闭集，而区间 \( [a, b] \) 是闭集但不是开集。

在 \( \mathbb{R} \) 中，唯一既开又闭的集合只有整个 \( \mathbb{R} \) 和空集 \( \emptyset \)。

因此，具有标准拓扑的实数空间 \( \mathbb{R} \) 是连通的。

再来看子空间 \( X = (0,1) \cup (2,3) \subset \mathbb{R} \)，它继承了实数集的诱导拓扑。

在这个子空间中，区间 \( (0,1) \) 与 \( (2,3) \) 都是既开又闭的。原因是：

因此，这两个区间都是开闭集。

由此可见，子空间 \( X \) 是非连通空间，因为它可以表示为两个互不相交、非空的开区间的并集，这两个区间共同覆盖了整个空间。