每个连通子集都包含在某个连通分量中
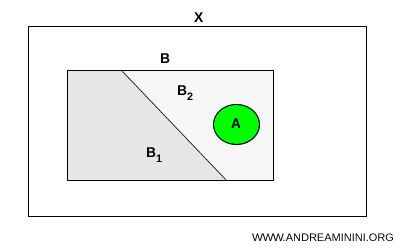
设 \( A \) 与 \( B \) 是拓扑空间 \( X \) 的子集,其中 \( A \) 是连通集,且 \( A \subset B \)。如果 \( B \) 在 \( X \) 中可以分离为两个子集 \( B_1 \) 与 \( B_2 \),那么 \( A \) 必然完全包含在这两个子集中的某一个之内:$$ A \subset B_1 \quad \text{或} \quad A \subset B_2 $$
这一结论可以用一句话概括:连通集不可能同时跨越一次分离的两个部分。
只要一个连通集处在一个可被分离的集合中,它就只能整体位于分离后的某一个部分,而不可能被"分开"。
为了形成直观理解,可以把连通集想象成一根完整且不断裂的绳子,放在一个信封里。如果信封被分成两个彼此隔离的隔间,而绳子保持完整,那么这根绳子只能完全落在其中一个隔间内。若它同时出现在两个隔间中,就意味着绳子被剪断了。连通性的作用正是排除这种情况,它保证集合不能跨越一次分离。
一个具体的例子
考虑最熟悉的拓扑空间:
$$ X = \mathbb{R} $$
以及 \( X \) 的如下子集:
$$ B = (-3,4) $$
集合 \( B \) 可以自然地分离为两个子集:
$$ B_1 = (-3,0), \qquad B_2 = (0,4) $$
它们互不相交:
$$ B_1 \cap B_2 = \varnothing $$
并且并集正好等于原集合:
$$ B_1 \cup B_2 = B $$
在 \( B \) 的子空间拓扑下,\( B_1 \) 与 \( B_2 \) 都是开集,因此它们构成了 \( B \) 在 \( X \) 中的一次分离。
现在取 \( B \) 的一个连通子集:
$$ A = (1,2) $$
显然 \( A \subset B_2 \),因此 \( A \) 完全位于这次分离的其中一个部分中,这正是前述结论的直接体现。
注。如果改取 \( A = (-1,1) \),就会得到 $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ 这样的形式。但这种情况在这里并不允许出现。原因在于,一旦 \( A \) 同时与 \( B_1 \) 和 \( B_2 \) 有非空交集,它本身就会被分成两个互不相交的部分,从而失去连通性。这与区间 \( (-1,1) \) 是连通集这一基本事实相矛盾。问题并不在于区间不连通,而在于它不可能在这种分离方式下作为一个整体包含在 \( B \) 中。
证明
假设
设 \( A \) 与 \( B \) 是拓扑空间 \( X \) 的子集,满足:
$$ A \subset X, \qquad B \subset X $$
并且:
- \( A \) 是连通集
- \( A \subset B \)
- \( B_1 \) 与 \( B_2 \) 构成了 \( B \) 在 \( X \) 中的一次分离
结论
则必有:
$$ A \subset B_1 \quad \text{或} \quad A \subset B_2 $$
证明思路
由于 \( B_1 \) 与 \( B_2 \) 构成了 \( B \) 的一次分离,我们知道:
- \( B_1 \cap B_2 = \varnothing \)
- \( B = B_1 \cup B_2 \)
- \( B_1 \) 与 \( B_2 \) 在 \( B \) 的子空间拓扑中都是开集
假设结论不成立,即 \( A \) 既不完全包含在 \( B_1 \) 中,也不完全包含在 \( B_2 \) 中,则:
$$ A \cap B_1 \neq \varnothing \qquad \text{且} \qquad A \cap B_2 \neq \varnothing $$
由于 \( A \subset B \),可得:
$$ A = A \cap B = (A \cap B_1) \cup (A \cap B_2) $$
而 \( B_1 \cap B_2 = \varnothing \) 意味着 \( A \cap B_1 \) 与 \( A \cap B_2 \) 也是互不相交的。进一步可以验证,这两个集合在 \( A \) 的子空间拓扑中都是非空开集。
因此,\( A \) 被分离成了两个互不相交的非空开集,这就构成了 \( A \) 的一次分离。
这与 \( A \) 是连通集的假设矛盾。
由此可知,反设不成立,结论必然成立:
$$ A \subset B_1 \quad \text{或} \quad A \subset B_2 $$
证明完毕。