连通空间：拓扑中的"不断裂世界"

从开集看连通性

直观地说，一个空间是连通的，意味着它是"完整的"：不能被切分成两个彼此独立、互不相交的部分。

一旦这种切分存在，我们就称 $(U, V)$ 为空间 $ X $ 的分离，此时 $ X $ 就是非连通的。

提示：这是用开集定义连通性的标准方式。后面我们还会看到，连通性和"道路连通性"（也叫"弧连通性"）虽然听起来相似，但其实不是一回事。

示例 1：三点构成的小空间

我们先来看一个简单的例子。设集合：

$$ X = {a, b, c} $$

现在在 $ X $ 上定义两种不同的拓扑：

• 拓扑 A：
  开集为 $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$
• 拓扑 B：
  开集为 $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$

问题是：这两个拓扑空间中哪个是连通的？

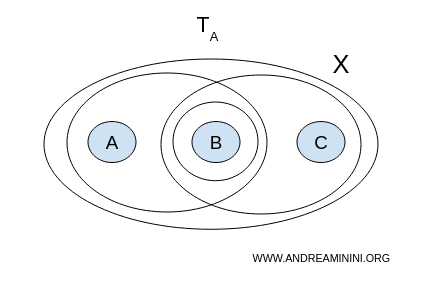
拓扑 A

我们尝试寻找一对分离 $(U, V)$，也就是两个互不相交、非空的开集，它们的并集覆盖整个空间 $ X $。

• $ U = {a,b}, V = {b,c} $ 不行，因为它们都包含 $ b $；
• $ U = {a,b}, V = {b} $ 也不行；
• $ U = {b}, V = {b,c} $ 仍然有重叠。

结果，没有任何一对满足条件的开集。因此，拓扑 A 下的 $ X $ 是连通的。

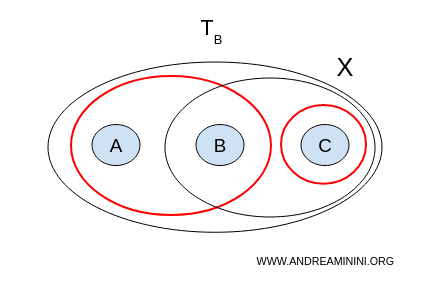
拓扑 B

现在看拓扑 B：

• $ U = {a,b}, V = {b,c} $ 依旧有重叠；
• $ U = {a,b}, V = {c} $ 互不相交、都非空，并且 $ U \cup V = {a,b,c} = X $。

这对开集 $( U = {a,b}, V = {c} )$ 就是一个分离。于是，拓扑 B 下的空间 $ X $ 是非连通的。

要点：连通性不仅取决于点集，还取决于拓扑结构。相同的点集，不同的拓扑，结果可能完全不同：A 是连通的，B 却断开了。

示例 2：从实数轴上去掉一个点

考虑集合：

$$ X = (-\infty, n) \cup (n, +\infty) $$

它表示实数轴上去掉一个点 $ n $ 后的部分，也就是：

$$ X = \mathbb{R} \setminus {n} $$

我们来判断它是否连通。

• $ U = (-\infty, n) $ 与 $ V = (n, +\infty) $ 都是开集；
• 它们互不相交；
• 它们都非空；
• 它们的并集 $ U \cup V = X $。

这正是分离的定义。因此，$ X = (-\infty, n) \cup (n, +\infty) $ 是非连通的。

提示：去掉一个点会让实数轴"断开"。左边和右边不再通过任何连续路径相连，因此这个空间不仅在拓扑意义上是非连通的，在道路意义上也不连通。

 连通 vs. 道路连通

很多初学者会混淆"连通空间"和"道路连通空间"，但它们其实是不同的概念。

• 拓扑连通性：不能用两个互不相交、非空的开集把空间分开。
• 道路连通性：任意两点之间存在一条完全位于空间内的连续路径。如果路径不重复点，就叫弧连通。

一般来说，道路连通 ⇒ 连通，但连通 ⇏ 道路连通。

有路径意味着空间"是一整块"，不会被割裂。但反过来并不成立。

经典例子：拓扑学家的正弦曲线

$$ S = { (x, \sin(1/x)) \mid x > 0 } \cup { (0, y) \mid -1 \le y \le 1 } $$

这个空间连通，因为无法用两个开集把它分开；但不是道路连通，因为不存在连续路径能从振荡曲线上的点连接到竖直线段上的点。

这说明，拓扑连通不一定意味着"可以走过去"。

补充说明

关于连通空间的进一步理解

• 定理：通过开闭集刻画连通空间
  拓扑空间 \( X \) 连通的充要条件是：在 \( X \) 中，唯一同时既开又闭（即 开闭集 或 clopen 集）的子集只有整个空间 \( X \) 和空集 \( \emptyset \)。

这一结果揭示了连通性的本质：如果一个空间无法被任何非平凡的开闭集分割，它就在拓扑意义上保持整体的连续性。后续章节将进一步探讨连通性在不同拓扑结构中的表现与应用。