利用开集将一个子集分离开来

在拓扑空间 $ X $ 中，我们常常关心一个子集是否能被开集"拆分"成两个互不相交的部分。具体来说，若存在开集 $ U $ 和 $ V $，满足以下条件，我们就说它们对 $ A $ 构成了分离：

简单来说，开集 $ U $ 与 $ V $ 在集合 $ A $ 内把它分成了两个独立的部分，各自占据一块区域，互不干扰。这是拓扑学中描述"子集被分离"的常用方式，也是理解连通性等概念的基础。

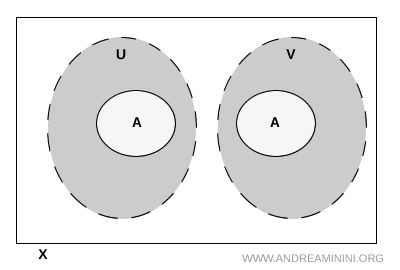
展示开集将子集 A 分离成两部分的示意图

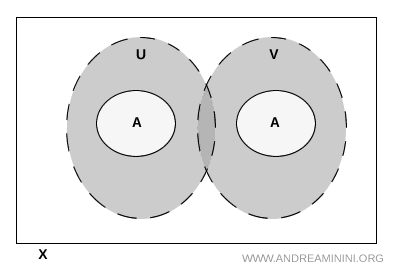
提示. 尽管我们要求 $ U $ 和 $ V $ 在 $ A $ 内互不相交，但它们在整个空间 $ X $ 中不必保持分离。它们完全可以在 $ A $ 之外交织在一起，只要不与 $ A $ 本身形成交集即可。
示意图：U 与 V 可在 A 外相交，但不与 A 有交集

一个直观的小例子

在实数轴 $ X = \mathbb{R} $ 上取两个彼此分开的闭区间：

$$ A = [-2,-1] \cup [1,2] $$

选择两个简单的开区间来"包住"它们：

$$ U = (-3,0) $$

$$ V = (0,3) $$

它们的大致位置如下：

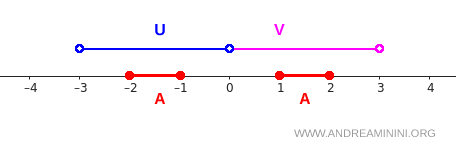
展示 U、V 与 A 的位置关系示意图

现在检查一下分离条件是否成立。

$ [-2,-1] $ 完全落在 $ U $ 中，$ [1,2] $ 完全落在 $ V $ 中，因此：

$$ A \subseteq U \cup V $$

两个开集都确实接触到了 $ A $：

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

并且它们在 $ A $ 的范围内完全没有交点：

$$ U \cap V \cap A = \varnothing $$

由此可见，在这个例子中，$ U $ 和 $ V $ 的确成功地把集合 $ A $ 分离成了两个互不相交的部分。这正是拓扑学讨论"连通或不连通"的核心思想之一。