通过公共交点理解连通性

设 \( C_1, C_2, \dots, C_n \subset X \) 是拓扑空间 \( X \) 中的一族连通子集，并且它们至少具有一个公共点：
\[ \bigcap_{i=1}^n C_i \neq \varnothing . \] 那么，它们的并集 \( \bigcup_{i=1}^n C_i \) 也是一个连通集。

直观地说，只要多个连通子集在某一点相遇，它们合在一起后依然构成一个整体，不会被"分开"。

这一结论依赖于一个关键前提，即这些集合存在公共交点。

注。条件 \( \bigcap_{i=1}^n C_i \neq \varnothing \) 是保证并集连通的充分条件，但并非必要条件。即使所有集合没有共同点，在某些结构下，它们的并集依然可能是连通的，例如当这些集合以"链式"方式相互连接时。

一个直观的例子

考虑平面 \( \mathbb{R}^2 \) 中的以下三个子集：

• \( C_1 \)：从 \( (-1,0) \) 到 \( (1,0) \) 的水平线段；
• \( C_2 \)：从 \( (0,-1) \) 到 \( (0,1) \) 的竖直线段；
• \( C_3 \)：连接 \( (-1,-1) \) 与 \( (1,1) \) 的对角线段。

这三个集合本身都是连通的。

并且它们都经过点 \( (0,0) \)。也就是说：

\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]

因此，它们的公共交集非空：

\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]

根据连通性的判据，它们的并集也是连通的：

\[ C_1 \cup C_2 \cup C_3 \]

三条线段在同一点相交，使整个图形自然地连成一个整体。

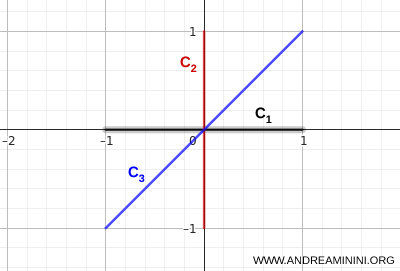
从这个并集中的任意一点出发，都可以沿着集合内部的路径到达任意其他点。

注。还有一些连通性判据并不要求所有集合共享同一个点。举例来说，如果一族集合按照"链式"方式相交，即满足 \( C_i \cap C_{i+1} \neq \varnothing \)，那么即使整体交集为空，并集 \( \bigcup_i C_i \) 仍然是连通的。更进一步，即便某些相邻集合彼此不相交，只要存在起到"桥梁"作用的集合，整体仍然可能保持连通。例如，三条线段围成一个三角形时，其整体交集为空，即 \( \bigcap_i C_i = \varnothing \)，但整个图形依然是连通的。

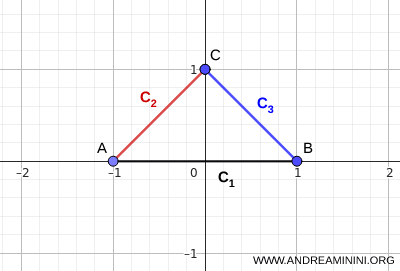
这个例子清楚地说明，只要结构合理，即使没有公共交点，整体仍然可以保持连通。

证明

设 \( X \) 为一个拓扑空间，\( \{C_i\}_{i \in I} \) 是其中的一族连通子集，并满足：

\[ \bigcap_{i \in I} C_i \neq \varnothing \]

我们采用反证法。假设并集

\[ C = \bigcup_{i \in I} C_i \]

不是连通的。

那么存在两个开集 \( U \) 与 \( V \)，它们构成 \( C \) 的一个分离，即：

• \( U \cap C \neq \varnothing \)
• \( V \cap C \neq \varnothing \)
• \( (U \cap C) \cap (V \cap C) = \varnothing \)
• \( C = (U \cap C) \cup (V \cap C) \)

由于假设中各集合 \( C_i \) 的交集非空，存在一点 \( x \in C \)，满足：

\[ x \in \bigcap_{i \in I} C_i \]

由于 \( U \) 与 \( V \) 构成对 \( C \) 的分离，点 \( x \) 必须属于其中之一。不妨设：

\[ x \in U \quad \text{且} \quad x \notin V \]

注意到每个 \( C_i \subset C \)，因此可写为：

\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]

其中 \( C_i \cap U \) 与 \( C_i \cap V \) 在子空间拓扑中都是开集，彼此不相交，且并集为整个 \( C_i \)。由于 \( C_i \) 本身是连通的，其中必有一个为空集。

因此，对任意 \( i \in I \)，必然有：

\[ C_i \subset U \quad \text{或} \quad C_i \subset V \]

又因为 \( x \in C_i \) 且 \( x \in U \)，所以不可能出现 \( C_i \subset V \) 的情况。

于是得到：

\[ C_i \subset U \quad \text{对所有 } i \in I \]

从而推出：

\[ \bigcup_{i \in I} C_i \subset U \]

这与假设 \( V \cap C \neq \varnothing \) 相矛盾。

因此，最初的假设不成立，从而可以断定并集 \( \bigcup_{i \in I} C_i \) 必然是连通的。

证毕。