用开集理解不连通性：一种清晰直观的刻画方式

换句话说，如果一个集合不连通，那么一定能找到两个彼此分离的开集，它们分别抓住了集合中的两个"部分"。这使我们可以仅凭开集结构来判断连通性，而不用依赖额外的工具。

示例一：两个区间的组合

来看实数轴上的集合：

$$ A = [0,1] \cup [2,3] $$

两个区间彼此之间有明显的空隙，所以集合当然是不连通的。

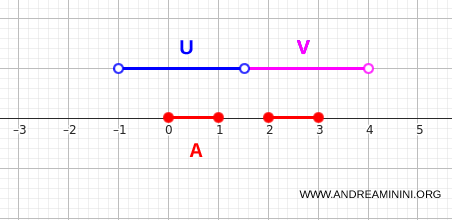
我们可以分别选择两个开区间：

• $U = (-1,1.5)$
• $V = (1.5,4)$

它们与 \(A\) 的交集正好覆盖两个独立的部分，并且在 \(A\) 中没有重叠：

$$ U \cap A = [0,1],\quad V \cap A = [2,3] $$

$$ (U \cap V) \cap A = \varnothing $$

由此可见，开集确实能清楚地将集合分离开来。

示例二：两个孤立点

来看更简单的一组数据：

$$ A = \{1,3\} $$

两个点互相之间没有任何连接，它们自然构成一个不连通的集合。

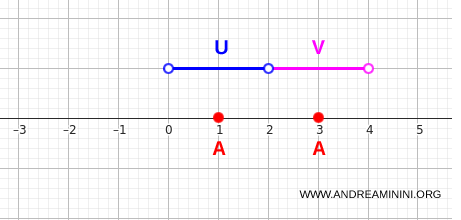
取开区间：

$$ U = (0,2),\quad V = (2,4) $$

它们分别只包含一个点：

$$ U \cap A = \{1\},\quad V \cap A = \{3\} $$

并且没有任何交叉：

$$ U \cap V \cap A = \varnothing $$

这再次展现了开集刻画不连通性的直接与有效。

示例三：被移除的 \(x\) 轴

考虑平面中去掉整条 \(x\) 轴的情形：

$$ A = \{(x,y)\in\mathbb{R}^2: y>0\} \cup \{(x,y): y<0\} $$

上半平面与下半平面完全由缺失的 \(x\) 轴隔开，因而毫无疑问是不连通的。

选择开集：

$$ U = \{(x,y): y>-1\},\quad V = \{(x,y): y<1\} $$

它们与 \(A\) 的交集覆盖两个半平面，且彼此在集合中没有重叠：

$$ (U \cap V) \cap A = \varnothing $$

这种例子很好地说明了在更高维空间中不连通性的表现方式。

核心思想：为什么这种刻画有效？

要理解其中的逻辑，可以将不连通看作"可分割性"。也就是说，如果一个集合能被分解成两个互不相交、各自非空的部分，那么它就是不连通的。

开集在这里的作用，是提供一种在整个空间中寻找这些分割方式的自然途径。

必要性

如果两个开集 \(U\) 和 \(V\) 能满足刻画条件，那么它们在 \(A\) 中形成的两个部分：

$$ P = U \cap A,\quad Q = V \cap A $$

刚好构成一个严格意义上的"分离"。因此 \(A\) 一定是不连通的。

充分性

反之，如果 \(A\) 已知是不连通的，那么它必然能写成：

$$ A = P \cup Q $$

其中 \(P\) 和 \(Q\) 非空、互不相交，并且都在子空间拓扑中是开集。

由于子空间开集来自母空间的开集，我们可以找到开集 \(U\) 和 \(V\) 使得：

$$ P = U \cap A,\quad Q = V \cap A $$

它们自然满足刻画的不连通性的各项条件。

总结

开集刻画不连通性的优点在于，它将抽象的连通概念转化为具体的集合关系。只要能找到两个适当的开集，将集合分割成互不相交且非空的两部分，那么该集合就是不连通的。

这不仅为理论研究提供了有力工具，也使许多实际问题中的连通性判断变得更加直观。