Teorem: Açık ve Kapalı (Clopen) Kümelerle Bağlantılı Uzayların Tanımlanması

Bir topolojik uzay \( X \), yalnızca hem açık hem de kapalı (yani clopen) olan alt kümeleri \( X \)'in kendisi ve boş küme \( \emptyset \) olduğunda bağlantılı (connected) olarak adlandırılır.

Başka bir deyişle, bir topolojik uzayda sadece önemsiz clopen kümeler bulunuyorsa, yani tüm uzay ve boş küme, bu uzay bağlantılı kabul edilir.

Yani aynı anda hem açık hem de kapalı olan, boş olmayan bir alt küme mevcut değilse, uzay bağlantılıdır.

Bu teorem, bir topolojik uzayın bağlantılı olup olmadığını anlamanın en temel yollarından biridir.

Temel Fikir

Topolojide, hem açık hem de kapalı bir alt küme varsa, bu küme uzayı iki ayrı, kesişmeyen ve boş olmayan açık parçaya ayırır. Böyle bir ayrım varsa, uzay artık tek parça değildir.

Eğer böyle önemsiz olmayan bir clopen küme mevcutsa, yani ne \( X \) ne de \( \emptyset \) değilse, uzay iki ayrı açık alt kümenin birleşimi olarak yazılabilir. Bu iki küme arasında hiçbir sürekli bağlantı bulunmaz.

Bu durumda uzay bağlantısız (disconnected) olur.

Tersine, eğer \( X \)'in tek clopen alt kümeleri \( X \) ve \( \emptyset \) ise, uzayı iki ayrık açık kümeye bölmek mümkün değildir. Dolayısıyla uzay bağlantılıdır.

Not: Her topolojik uzayda tüm küme \( X \) ve boş küme \( \emptyset \) her zaman hem açık hem de kapalıdır.

Örnek 1 - Sonlu bir uzayda bağlantısızlık

\( X = \{ a, b, c, d \} \) kümesini ve şu şekilde tanımlanan topoloji \( T \)'yi ele alalım: \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \).

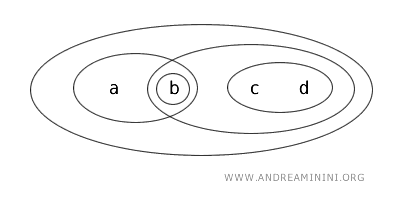
Bu durumda \( \{ a, b \} \) alt kümesi hem açık hem de kapalı, yani clopen'dir.

• Açıktır çünkü topoloji \( T \)'de açık küme olarak tanımlanmıştır.
• Kapalıdır çünkü tamamlayanı \( X \setminus \{ a, b \} = \{ c, d \} \) de \( T \)'de açıktır.

Dolayısıyla \( (X, T) \) uzayı bağlantısızdır. Yani uzayı iki açık ve birbirinden ayrık parçaya ayırmak mümkündür: \( \{ a, b \} \) ve \( \{ c, d \} \).

Bu örnek bize şunu gösterir: Önemsiz olmayan tek bir clopen küme bile uzayın bağlantısız olduğunu kanıtlamak için yeterlidir.

Örnek 2 - Gerçek sayılar kümesi

Şimdi açık aralıklar \( (a, b) \) tarafından oluşturulan standart topoloji (standard topology) ile donatılmış gerçek sayılar kümesini \( \mathbb{R} \) ele alalım.

Bu topolojide \( (a, b) \) aralıkları açıktır ama kapalı değildir. \( [a, b] \) aralıkları ise kapalıdır ama açık değildir.

\( \mathbb{R} \)'de hem açık hem de kapalı olan tek kümeler \( \mathbb{R} \)'nin kendisi ve \( \emptyset \)'tir.

Bu nedenle, standart topolojiye sahip \( \mathbb{R} \) uzayı bağlantılıdır. Gerçek sayılar düzlemi tek bir sürekli bütün oluşturur, ikiye bölünemez.

Örnek 3 - Ayrık iki aralıktan oluşan alt uzay

Şimdi \( X = (0,1) \cup (2,3) \subset \mathbb{R} \) alt uzayını, \( \mathbb{R} \)'nin standart topolojisinden türetilen (induced) topolojiyle ele alalım.

Bu durumda \( (0,1) \) ve \( (2,3) \) alt kümeleri hem \( X \)'te açık hem de kapalıdır. Çünkü her birinin \( X \) içindeki tamamlayanı diğer açık aralıktır. Özellikle:

• \( X \)'te \( (0,1) \)'in tamamlayanı \( (2,3) \)'tür ve bu \( X \)'te açıktır.
• \( X \)'te \( (2,3) \)'ün tamamlayanı \( (0,1) \)'dir ve bu da \( X \)'te açıktır.

Dolayısıyla her iki alt küme de clopen'dir.

Bu durumda \( X \) uzayı bağlantısızdır. Çünkü \( X \), iki ayrık ve boş olmayan açık alt kümenin birleşimidir: \( (0,1) \) ve \( (2,3) \).

Bu örnek, bağlantısızlığın sezgisel anlamını açıkça gösterir: Uzay iki ayrı bölgeye ayrılmıştır ve birinden diğerine geçiş yapmanın sürekli bir yolu yoktur.