Her bağlantılı altküme tek bir bağlantılı bileşen içinde bulunur
\( X \) bir topolojik uzay olsun. \( A \) ve \( B \), \( X \)'in altkümeleri olsun. \( A \) bağlantılı ve \( A \subset B \) olsun. Eğer \( B \), \( X \) içinde \( B_1 \) ve \( B_2 \) olmak üzere iki altkümeye ayrılabiliyorsa, o zaman \( A \), bu iki altkümeden yalnızca birinin içinde bütünüyle bulunmak zorundadır: $$ A \subset B_1 \quad \text{ya da} \quad A \subset B_2 $$
Başka bir deyişle, bağlantılı bir küme, bir ayrımın her iki tarafına aynı anda yayılmış olamaz.
Eğer bağlantılı bir altküme, iki ayrık parçaya bölünmüş bir kümenin içinde yer alıyorsa, bu parçalardan yalnızca birinin içinde tamamen bulunur.
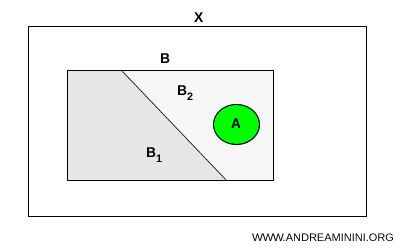
Sezgisel bir bakış açısıyla, bağlantılı bir kümeyi tek parça, kopmamış bir ip gibi düşünebiliriz. Bu ip bir zarfın içine yerleştirilsin. Zarf iki ayrık bölmeye ayrıldığında ip hâlâ bütünlüğünü koruyorsa, ip zorunlu olarak bu bölmelerden yalnızca birinin içinde kalır. Aksi hâlde ipin kopması gerekirdi. Bağlantılılık kavramı, bir kümenin bir ayrımın iki tarafına birden yayılmasını tam olarak bu şekilde engeller.
Somut bir örnek
Şimdi bu ilkeyi basit bir örnek üzerinden görelim.
Aşağıdaki topolojik uzayı ele alalım:
$$ X = \mathbb{R} $$
ve bu uzayın şu altkümesini inceleyelim:
$$ B = (-3,4) $$
Bu küme, aşağıdaki iki altkümeye ayrılabilir:
$$ B_1 = (-3,0) $$
$$ B_2 = (0,4) $$
Bu iki altküme birbirinden ayrıdır:
$$ B_1 \cap B_2 = \varnothing $$
ve birleşimleri tam olarak \( B \)'yi verir:
$$ B_1 \cup B_2 = B $$
Ayrıca, her iki küme de \( B \) üzerindeki altuzay topolojisine göre açıktır.
Bu nedenle \( B_1 \) ve \( B_2 \), \( X \) içinde \( B \)'nin bir ayrımını oluşturur.
Şimdi \( B \)'nin bağlantılı bir altkümesini ele alalım:
$$ A = (1,2) $$
\( A \subset B_2 \) olduğundan, \( A \) ayrımı oluşturan iki altkümeden yalnızca birinin içinde tamamen yer almaktadır.
Not. Bunun yerine \( A = (-1,1) \) alındığını düşünelim. Bu durumda $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ olur. Ancak bu durum mümkün değildir. Çünkü \( B_1 \) ve \( B_2 \), \( B \)'nin bir ayrımını oluşturur ve bağlantılı bir altküme bu ayrımın iki parçasına birden dağılamaz. Eğer böyle bir dağılım mümkün olsaydı, \( A \) da kendi içinde bir ayrım kabul ederdi. Bu ise \( (-1,1) \) aralığının bağlantılı olmasıyla çelişir. Sorun, \( (-1,1) \)'in bağlantılı olmaması değildir. Asıl nokta, \( B \) bu şekilde ayrılmışken, \( (-1,1) \)'in \( B \)'nin bir altkümesi olarak yer alamamasıdır.
İspat
Varsayımlar
\( A \) ve \( B \), \( X \) topolojik uzayının altkümeleri olsun:
$$ A \subset X \quad \text{ve} \quad B \subset X $$
Aşağıdaki varsayımlar altında çalışıyoruz:
- \( A \) bağlantılıdır
- \( A \subset B \)
- \( B_1 \) ve \( B_2 \), \( X \) içinde \( B \)'nin bir ayrımını oluşturur
İddia
Bu varsayımlar altında \( A \), ya \( B_1 \)'in ya da \( B_2 \)'nin altkümesidir:
$$ A \subset B_1 \quad \text{ya da} \quad A \subset B_2 $$
İspat
Varsayım gereği, \( B_1 \) ve \( B_2 \), \( X \) içinde \( B \)'nin bir ayrımını oluşturur. Bu da şu özellikleri beraberinde getirir:
- \( B_1 \cap B_2 = \varnothing \), yani kümeler ayrıdır
- \( B = B_1 \cup B_2 \), yani birleşimleri \( B \)'nin tamamını verir
- \( B_1 \) ve \( B_2 \), \( B \) üzerindeki altuzay topolojisine göre açıktır
Şimdi çelişki yoluyla ilerleyelim ve \( A \)'nın ne \( B_1 \)'in ne de \( B_2 \)'nin içinde bütünüyle yer aldığını varsayalım.
$$ A \cap B_1 \neq \varnothing \qquad \text{ve} \qquad A \cap B_2 \neq \varnothing $$
\( A \subset B \) olduğundan şu eşitlik elde edilir:
$$ A = A \cap B = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$
\( B_1 \) ve \( B_2 \) ayrık olduğundan, \( A \cap B_1 \) ile \( A \cap B_2 \) de ayrık kümelerdir.
Dolayısıyla bu iki küme, ayrık, boş olmayan ve \( A \) üzerindeki altuzay topolojisine göre açık altkümeler olup, birlikte \( A \)'nın bir ayrımını oluşturur.
Bu sonuç, \( A \)'nın bağlantılı olduğu varsayımıyla çelişir.
O hâlde başlangıçtaki varsayım geçersizdir ve sonuç olarak:
$$ A \subset B_1 \quad \text{ya da} \quad A \subset B_2 $$
sonucuna ulaşılır.
İspat tamamlanmıştır.
Ve devamı.