Topolojik uzaylarda bağlantısız kümeleri anlamak: açık kümelerle yapılan ayrım
Topolojik bir uzay \(X\) içinde yer alan bir altküme \(A \subset X\) olsun. Bu kümenin bağlantısız olup olmadığını anlamanın etkili yollarından biri, onu iki açık küme yardımıyla ayırıp ayıramadığımızı kontrol etmektir. Eğer \(X\)’te aşağıdaki koşulları sağlayan iki açık küme \(U\) ve \(V\) bulunuyorsa, \(A\) bağlantısızdır:
- \(A\), \(U \cup V\)’nin içindedir,
- \(U\) ve \(V\), \(A\)’dan en az birer nokta içerir,
- \(U \cap V\) içinde \(A\)’ya ait bir nokta yoktur.
Bu fikir oldukça sezgiseldir: Eğer bir kümeyi, uzayın iki açık bölgesine dağıtıp bu bölgelerin \(A\) üzerinde hiç kesişmediğini gösterebiliyorsak, kümenin içinde bir bağlantı yoktur. Önemli olan yalnızca açık kümelerle çalışmaktır; daha gelişmiş araçlara ihtiyaç duyulmaz.
Örnek 1: Gerçek doğru üzerindeki iki aralık
Basit bir örnekle başlayalım:
$$ A = [0,1] \cup [2,3] \subset \mathbb{R} $$
Bu iki kapalı aralık arasında, \(A\)’nın içinde kalan bir yol olmadığı açıkça görülür. Bir aralıktan diğerine geçmek için kümenin dışına çıkmak gerekir.
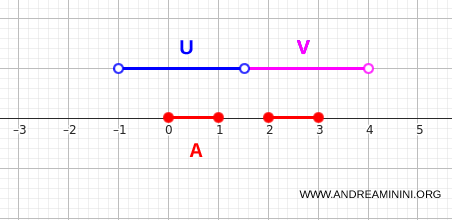
Bunu açık kümelerle doğrulamak oldukça kolaydır. Aşağıdaki iki açık küme işimizi görür:
- \(U = (-1,1.5)\)
- \(V = (1.5,4)\)
Kesişimler şöyledir:
$$ U \cap A = [0,1] $$
$$ V \cap A = [2,3] $$
$$ (U \cap V) \cap A = \varnothing $$
Böylece aralıkların birbirinden tamamen ayrıldığı netleşir.
Örnek 2: İki noktanın ayrılması
Daha küçük ama açıklayıcı bir örnek:
$$ A = \{1, 3\} \subset \mathbb{R} $$
Bu küme iki izole noktadan oluşur; biri diğerine bağlı değildir.
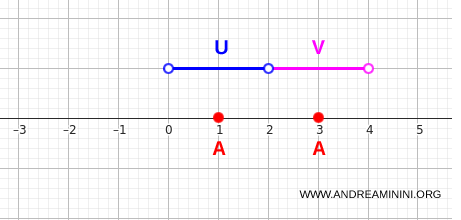
Aşağıdaki seçim ayrımı açıkça ortaya koyar:
$$ U = (0,2) \qquad V = (2,4) $$
İlgili kesişimler:
$$ U \cap A = \{1\} $$
$$ V \cap A = \{3\} $$
$$ U \cap V \cap A = \varnothing $$
İki nokta açık kümelerle tamamen ayrıldığı için küme bağlantısızdır.
Örnek 3: İki yarı düzlem
Şimdi düzlemde daha ilgi çekici bir durum inceleyelim. \(\mathbb{R}^2\)’den \(x\)-eksenini çıkardığımızı düşünelim:
$$ A = \{(x,y) : y>0\} \cup \{(x,y) : y<0\} $$
Böylece üst ve alt yarı düzlemler elde edilir. Bu iki bölge, aralarında artık kümenin parçası olmayan bir doğruyla tamamen ayrılmıştır.
Aşağıdaki açık kümeler durumu netleştirir:
$$ U = \{(x,y) : y> -1\} $$
$$ V = \{(x,y) : y< 1\} $$
- \(U \cap A\) üst yarı düzlemi,
- \(V \cap A\) alt yarı düzlemi kapsar.
Bu iki açık bölgenin \(A\) üzerinde ortak noktası olmadığından ayrım kesinleşir.
Kanıtın özeti
Bu karakterizasyon iki yönlüdür. Eğer \(A\), iki açık küme ile ayrılabiliyorsa bağlantısızdır. Tersine, \(A\) bağlantısızsa mutlaka böyle açık kümeler bulunabilir. Altuzay topolojisinde açık olan her parça, uzaydaki bir açık kümenin \(A\) ile kesişimi olarak yazılabilir. Böylece iki parça, iki açık kümeye karşılık gelir.
Sonuç
Bir kümenin bağlantısız olup olmadığını anlamak, karmaşık araçlar gerektirmez. Yalnızca açık kümelerle çalışmak yeterlidir. Eğer bir küme, birbirinden ayrık ve altuzay topolojisinde açık iki parçaya ayrılabiliyorsa bağlantısızdır. Bu yaklaşım hem sezgiseldir hem de topolojinin temel kavramlarına dayanır, bu yüzden öğrenme sürecini oldukça anlaşılır kılar.