Bağlantılı Uzay Nedir?

Açık kümelerle açıklama

Basitçe söylemek gerekirse, bir uzay, açık kümelere bölündüğünde parçalanamıyorsa topolojik olarak bağlantılıdır. Eğer parçalanabiliyorsa, uzay bağlantısız olur ve bu durum $(U, V)$ çiftiyle ifade edilir; bu çift $(X)$ uzayının ayrımı olarak adlandırılır.

Not. Bu, açık kümeler kullanılarak yapılan topolojik bağlantılılık tanımıdır. "Yol bağlantılılık" veya "yay bağlantılılık" kavramlarıyla aynı değildir. İleride göreceğimiz gibi, bazı durumlarda bu iki kavram birbirinden farklı sonuçlar verebilir.

Basit bir örnek

Üç elemandan oluşan bir küme düşünelim:

$$ X = {a, b, c} $$

Bu küme üzerinde iki farklı topoloji tanımlayalım:

• Topoloji A:
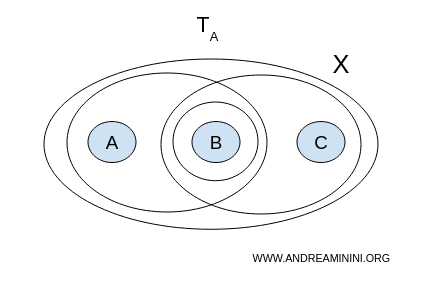
  Açık kümeler şöyle olsun: $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$
• Topoloji B:
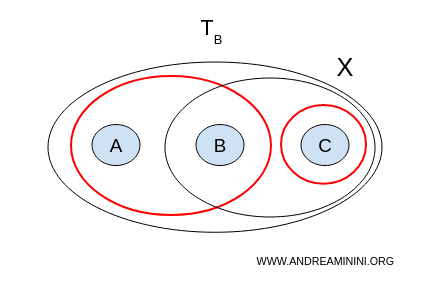
  Açık kümeler: $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$

Şimdi soralım: Hangi uzay bağlantılıdır?

1. Topoloji A

$ \mathcal{T}_A $ içinde boş olmayan ve ayrık iki açık küme arayalım. Amacımız, birleşimleri $ X $'i tamamen kapsayan bir çift $(U, V)$ bulmaktır.

• $ U = {a,b}, V = {b,c} $ ayrık değildir, çünkü her ikisi de $ b $'yi içerir.
• $ U = {a,b}, V = {b} $ yine ayrık değildir.
• $ U = {b}, V = {b,c} $ de ayrık değildir.

Bu durumda, $ X $'i tamamen kapsayan ayrık iki açık küme bulamıyoruz. Dolayısıyla, $ X $ uzayı Topoloji A altında bağlantılıdır.

2. Topoloji B

$ \mathcal{T}_B $ topolojisinde aynı şeyi deneyelim:

• $ U = {a,b}, V = {b,c} $ ayrık değildir, çünkü ikisi de $ b $'yi içerir.
• $ U = {a,b}, V = {c} $ ayrık ve boş olmayan iki kümedir. Ayrıca birleşimleri $ X $'i tamamen kapsar: $ U \cup V = {a,b,c} = X $.

Bu çift, ayrım koşullarını sağladığı için, $ X $ uzayı Topoloji B altında bağlantısızdır.

Not. Bu örnek, bağlantılılığın yalnızca kümenin kendisine değil, topolojinin yapısına da bağlı olduğunu açıkça gösterir. Aynı nokta kümesi bile farklı topolojiler altında farklı özellikler gösterebilir: biri bağlantılılığı korurken, diğeri ortadan kaldırabilir.

Gerçek sayılarla bir örnek

$ n $ sabit bir reel sayı (örneğin $ n = 0 $) olmak üzere şu kümeyi ele alalım:

$$ X = (-\infty, n) \cup (n, +\infty) $$

Bu, bir noktası çıkarılmış reel doğruyu temsil eder: $$ X = \mathbb{R} \setminus {n} $$

$ U = (-\infty, n) $ ve $ V = (n, +\infty) $ kümeleri hem açık hem de ayrık ve boş değildir. Ayrıca birleşimleri tam olarak $ X $'i verir:

$$ U \neq \emptyset, \quad V \neq \emptyset, \quad U \cap V = \emptyset, \quad U \cup V = X $$

Bu, tanım gereği bir ayrımdır. Dolayısıyla bu uzay bağlantısızdır.

Not. Gerçek doğrudan tek bir noktanın çıkarılması bile sürekliliği bozar. Doğru, $ n $ noktasının solunda ve sağında iki ayrı parçaya ayrılır. Bu parçalar arasında artık herhangi bir sürekli yol yoktur. Bu nedenle uzay hem bağlantısız hem de yol bağlantılı değildir.

Bağlantılılık ve yol bağlantılılık farkı

Topolojik bağlantılılık ile yol bağlantılılık birbirinden farklı kavramlardır.

Bir uzay, bağlantılı olabilir ama içinde herhangi iki noktayı sürekli bir yol ile birleştirmek mümkün olmayabilir.

• Topolojik bağlantılılık:
  Uzay, birleşimleri tüm uzayı kapsayan iki ayrık, boş olmayan açık altkümeye ayrılamaz.
• Yol bağlantılılık:
  Uzaydaki her iki nokta arasında, tamamen uzayın içinde kalan sürekli bir yol bulunur. Eğer yol hiçbir noktadan iki kez geçmiyorsa, uzay yay bağlantılı olarak adlandırılır.

Genel kural şudur: Her yol bağlantılı uzay bağlantılıdır, ancak her bağlantılı uzay yol bağlantılı değildir.

İki nokta arasında sürekli bir yol varsa, uzayı iki ayrı açık bölgeye "kesmek" mümkün değildir. Ancak tersi doğru değildir; bağlantılı ama yol bağlantılı olmayan uzaylar da vardır.

Örnek. Klasik bir örnek topoloğun sinüs eğrisidir: $$ S = { (x, \sin(1/x)) \mid x > 0 } \cup { (0, y) \mid -1 \le y \le 1 } $$ Bu uzay, iki ayrık açık kümeye ayrılamadığı için bağlantılıdır, ancak salınımlı eğri üzerindeki bir nokta ile dikey doğru üzerindeki bir noktayı birleştiren sürekli bir yol bulunmadığından yol bağlantılı değildir.

Bu örnek, topolojide bağlantılılık kavramının ne kadar zengin ve çok boyutlu olduğunu açıkça gösterir.

Notlar

Bağlantılı uzaylar hakkında ek açıklamalar

• Teorem: Açık ve Kapalı (Clopen) Kümelerle Bağlantılı Uzayların Tanımlanması
  Bir topolojik uzay \( X \), yalnızca hem açık hem de kapalı (yani clopen) olan alt kümeleri \( X \)’in kendisi ve boş küme \( \emptyset \) olduğunda bağlantılı kabul edilir.

Buna benzer başka özellikler ve sonuçlar da topolojide ayrıntılı biçimde incelenebilir.