Ortak Kesişim Yoluyla Bağlantılılık

\( C_1, C_2, \dots, C_n \subset X \) olmak üzere, \( X \) bir topolojik uzay ve bu kümeler bağlantılı alt kümeler olsun. Eğer bu kümelerin en az bir ortak noktası varsa, yani \[
\bigcap_{i=1}^n C_i \neq \varnothing , \] o hâlde birleşimleri \( \bigcup_{i=1}^n C_i  \) de bağlantılıdır.

Başka bir deyişle, bir topolojik uzayda birden fazla bağlantılı alt küme ortak en az bir noktayı paylaşıyorsa, bu kümelerin birleşimi de bağlantılı bir yapı oluşturur.

Bu sonuç, bağlantılılığın korunmasını sağlayan temel bir ilkedir ve kümelerin ortak bir noktada kesiştiği varsayımına dayanır.

Not. \( \bigcap_{i=1}^n C_i \neq \varnothing \) koşulu, birleşimin bağlantılı olması için yeterli bir koşuldur; ancak zorunlu değildir. Başka bir deyişle, tüm kümeler tek bir ortak noktada kesişmese bile birleşim yine bağlantılı olabilir. Bu durum özellikle zincir biçimli kesişimlerde ortaya çıkar.

Somut bir örnek

\( \mathbb{R}^2 \) düzleminde aşağıdaki alt kümeleri ele alalım:

• \( C_1 \): \( (-1,0) \) ile \( (1,0) \) arasındaki yatay doğru parçası,
• \( C_2 \): \( (0,-1) \) ile \( (0,1) \) arasındaki düşey doğru parçası,
• \( C_3 \): \( (-1,-1) \) ile \( (1,1) \) noktalarını birleştiren köşegen doğru parçası.

Bu kümelerin her biri tek başına bağlantılıdır.

Ayrıca hepsi ortak olarak \( (0,0) \) noktasını içerir. Gerçekten de:

\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]

Dolayısıyla ortak kesişim boş değildir:

\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]

Bu nedenle, bağlantılılık ölçütüne göre bu üç kümenin birleşimi de bağlantılıdır:

\[ C_1 \cup C_2 \cup C_3  \]

Üç doğru parçası aynı merkez noktada kesişir. Bu yapı, birleşimin bağlantılı olmasını açık biçimde garanti eder.

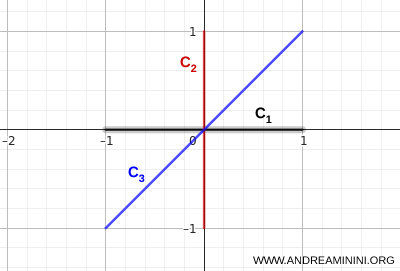
Bu birleşim üzerinde bulunan herhangi bir noktadan, yalnızca birleşimin içinde kalarak diğer tüm noktalara ulaşmak mümkündür.

Not. Bağlantılılık için tüm kümelerin ortak bir noktada kesişmesi her zaman gerekmez. Örneğin, \( C_i \) kümeleri bağlantılıysa ve ardışık biçimde kesişiyorlarsa, yani \( C_i \cap C_{i+1} \neq \varnothing \) ise, \( \bigcup_i C_i \) birleşimi, \( \bigcap_i C_i = \varnothing \) olsa bile bağlantılıdır.

Bazı durumlarda ise ardışık kümeler doğrudan kesişmese bile, aradaki başka kümeler bağlantıyı sağlayan birer "köprü" görevi üstlenir.

Örneğin, bir üçgen oluşturan üç doğru parçasını düşünelim. Bu durumda \( \bigcap_i C_i = \varnothing \) olmasına rağmen birleşim bağlantılıdır.

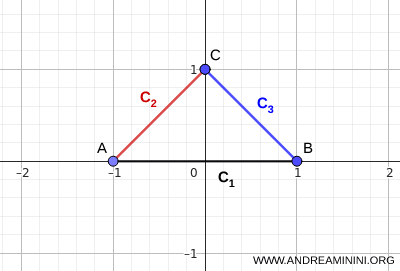
Bu örnek, zincirleme kesişimin bağlantılılığı garanti etmeye yeterli olduğunu açık biçimde gösterir.

İspat

\( X \) bir topolojik uzay ve \( \{C_i\}_{i \in I} \), bu uzayda yer alan, ortak kesişimi boş olmayan bağlantılı alt kümeler ailesi olsun:

\[ \bigcap_{i \in I} C_i \neq \varnothing \]

Aksini varsayalım ve birleşimin

\[ C = \bigcup_{i \in I} C_i \]

bağlantılı olmadığını kabul edelim.

Eğer \( C \) bağlantılı değilse, onu ayıran iki açık küme vardır. Bunları \( U \) ve \( V \) ile gösterelim. Bu durumda:

• \( U \cap C \neq \varnothing \)
• \( V \cap C \neq \varnothing \)
• \( (U \cap C) \cap (V \cap C) = \varnothing \)
• \( C = (U \cap C) \cup (V \cap C) \)

Varsayıma göre ortak kesişim boştur değildir:

\[ \bigcap_{i \in I} C_i \neq \varnothing \]

Dolayısıyla tüm kümelerde bulunan bir nokta vardır:

\[ x \in \bigcap_{i \in I} C_i \]

Bu nokta, ayırma tanımı gereği ya \( U \) içinde ya da \( V \) içinde yer alır; her ikisinde birden bulunamaz. Genelliği bozmadan,

\[ x \in U \quad \text{ve} \quad x \notin V \]

olduğunu varsayalım.

Her \( C_i \subset C \) olduğundan, şu ayrışımı yazabiliriz:

\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]

Burada \( C_i \cap U \) ve \( C_i \cap V \), \( C_i \) üzerinde açık, ayrık ve birlikte tüm \( C_i \)'yi örten alt kümelerdir. Ancak \( C_i \) bağlantılı olduğundan, bu iki kümeden biri zorunlu olarak boştur.

Dolayısıyla her \( C_i \) bütünüyle ya \( U \) ya da \( V \) içinde yer alır:

\[ C_i \subset U \quad \text{ya da} \quad C_i \subset V \]

Fakat \( x \in C_i \) ve aynı zamanda \( x \in U \) olduğuna göre, \( C_i \subset V \) olması mümkün değildir.

Buna göre:

\[ C_i \subset U \quad \text{tüm } i \in I \text{ için} \]

Dolayısıyla:

\[ \bigcup_{i \in I} C_i \subset U \]

Bu durum ise \( V \cap C \neq \varnothing \) varsayımıyla çelişir.

Ortaya çıkan bu çelişki, başlangıç varsayımının yanlış olduğunu gösterir. Dolayısıyla \( \bigcup_{i \in I} C_i \) kümesi bağlantılıdır.

Böylece ispat tamamlanmış olur.