Alt Kümenin Açık Kümelerle Ayrılması

Bir topolojik uzay $ X $ içinde $ A $ bir alt küme olsun. $ X $ içindeki açık kümeler $ U $ ve $ V $, aşağıdaki koşullar sağlandığında $ A $'nın bir ayrımı (separation) olarak kabul edilir:

$ A $'yı birlikte örtmeleri \[ A \subseteq U \cup V \]
Her birinin $ A $ ile boş olmayan bir kesişime sahip olması \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
$ A $ üzerinde ayrık olmaları \[ U \cap V \cap A = \varnothing \]

Bu koşullar sağlandığında $ A $ kümesinin iki ayrı parçaya bölündüğünü görürüz. Bu parçaların biri tamamen $ U $'nun içinde, diğeri ise $ V $'nin içindedir. Önemli olan, bu iki parçanın $ A $ üzerinde hiçbir noktada kesişmemesidir. Topolojide bir alt kümenin "ayrılmış" sayılması tam olarak bu durumu ifade eder.

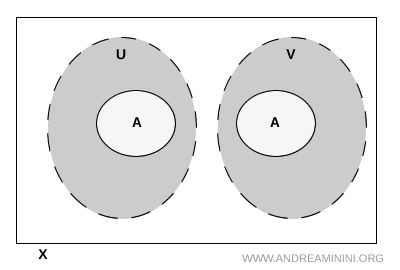
A kümesinin U ve V açık kümeleriyle ayrılmasını gösteren topolojik diyagram

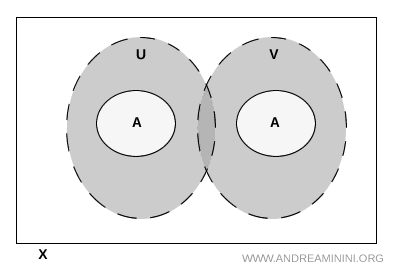
Nota. $ U $ ve $ V $ kümelerinin tüm uzay $ X $ içinde ayrık olması gerekmez. $ A $'nın dışında kesişmeleri mümkündür. Esas nokta, bu kesişimin $ A $ kümesine hiç dokunmamasıdır.
U ve V'nin A kümesinin dışında kesişebileceğini gösteren topolojik diyagram

Uygulamalı Bir Örnek

Şimdi bu tanımı somut bir örnek üzerinde inceleyelim. Standart topolojiye sahip gerçek sayılar uzayını, yani $ X = \mathbb{R} $'yi ele alalım. $ A $ kümesi iki ayrık kapalı aralıktan oluşsun:

$$ A = [-2,-1] \cup [1,2] $$

Bu kez $ X $ içinde iki açık küme tanımlıyoruz:

$$ U = (-3,0) $$

$$ V = (0,3) $$

Bu kümelerin konumu ve birbirleriyle ilişkisi aşağıdaki grafikte görülebilir:

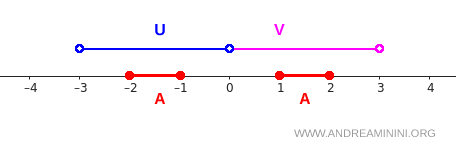
U ve V açık kümelerinin A alt kümesiyle ilişkisini gösteren grafik

Artık ayrım koşullarını adım adım kontrol edebiliriz.

$ [-2,-1] $ aralığı tamamen $ U $'nun içindedir.

$ [1,2] $ aralığı ise tamamen $ V $'de yer alır.

Böylece şunu doğrulamış oluruz:

$$ A \subseteq U \cup V $$

Her iki açık küme de $ A $ ile boş olmayan bir kesişime sahiptir:

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

Son olarak, $ U $ ve $ V $ kümeleri $ A $ üzerinde ortak bir noktaya sahip değildir:

$$ U \cap V \cap A = \varnothing $$

Bütün bu sonuçlar birlikte ele alındığında, $ U $ ve $ V $ açık kümelerinin $ A $ alt kümesini topolojik olarak ayıran düzenli bir ayrım oluşturduğu açıkça görülür.