Связность при наличии общей точки

Пусть \( C_1, C_2, \dots, C_n \subset X \) - семейство связных подмножеств топологического пространства \( X \), которые имеют хотя бы одну общую точку: \[
\bigcap_{i=1}^n C_i \neq \varnothing . \] Тогда их объединение \( \bigcup_{i=1}^n C_i  \) также является связным множеством.

Иначе говоря, если несколько связных подмножеств пространства \( X \) имеют хотя бы одну общую точку, то их объединение сохраняет связность.

Ключевую роль здесь играет условие непустоты общего пересечения всех множеств.

Примечание. Условие \( \bigcap_{i=1}^n C_i \neq \varnothing \) является достаточным для связности объединения \( \bigcup_{i=1}^n C_i \), но не является необходимым. Объединение связных множеств может оставаться связным и без общей точки. Это часто происходит в ситуациях, связанных с так называемыми цепочечными пересечениями.

Наглядный пример

Рассмотрим следующие подмножества пространства \( \mathbb{R}^2 \):

• \( C_1 \): горизонтальный отрезок от точки \( (-1,0) \) до точки \( (1,0) \)
• \( C_2 \): вертикальный отрезок от точки \( (0,-1) \) до точки \( (0,1) \)
• \( C_3 \): диагональный отрезок, соединяющий точки \( (-1,-1) \) и \( (1,1) \)

Каждое из этих множеств является связным.

Кроме того, все они проходят через одну и ту же точку \( (0,0) \). В самом деле,

\[ (0,0) \in C_1 \cap C_2 \cap C_3 \]

Следовательно, их общее пересечение непусто:

\[ \bigcap_{i=1}^3 C_i = \{(0,0)\} \]

Отсюда непосредственно следует, что их объединение является связным множеством:

\[ C_1 \cup C_2 \cup C_3  \]

Все три отрезка пересекаются в одной точке, и благодаря этому между любыми двумя точками объединения существует непрерывный путь, целиком лежащий внутри него.

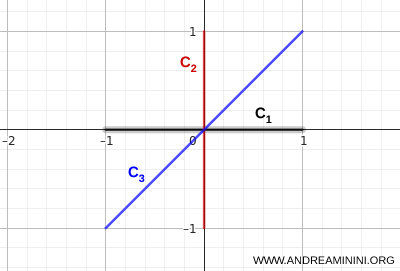
Иначе говоря, из любой точки одного отрезка можно добраться до любой другой точки, не покидая объединения.

Примечание. Существуют и другие критерии связности, не требующие, чтобы все множества \( C_i \) имели общую точку. Например, если множества \( C_i \) связны и пересекаются «по цепочке», то есть выполняется условие \( C_i \cap C_{i+1} \neq \varnothing \), то их объединение \( \bigcup_i C_i \) также является связным, даже если \( \bigcap_i C_i = \varnothing \). Однако и цепочечное пересечение не является необходимым условием: объединение может оставаться связным даже тогда, когда некоторые соседние множества не пересекаются напрямую, при условии, что другие элементы семейства выполняют роль «мостов». В качестве иллюстрации можно рассмотреть три отрезка, образующие треугольник. Их общее пересечение пусто, \( \bigcap_i C_i = \varnothing \), но объединение остаётся связным.

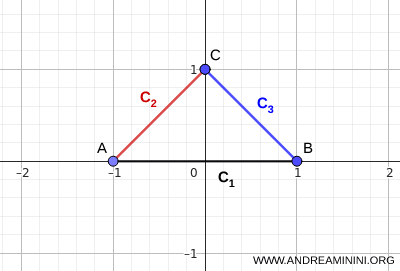
Этот пример наглядно показывает, что цепочечное пересечение является достаточным условием связности объединения.

Доказательство

Пусть \( X \) - топологическое пространство, а \( \{C_i\}_{i \in I} \) - семейство связных подмножеств пространства \( X \), имеющих непустое общее пересечение:

\[ \bigcap_{i \in I} C_i \neq \varnothing \]

Предположим противное, а именно что объединение

\[ C = \bigcup_{i \in I} C_i \]

не является связным.

Тогда существуют два открытых множества \( U \) и \( V \), образующие разбиение множества \( C \), то есть выполняются условия:

• \( U \cap C \neq \varnothing \)
• \( V \cap C \neq \varnothing \)
• \( (U \cap C) \cap (V \cap C) = \varnothing \)
• \( C = (U \cap C) \cup (V \cap C) \)

Поскольку пересечение всех множеств \( C_i \) непусто, существует точка \( x \in C \), принадлежащая каждому из них:

\[ x \in \bigcap_{i \in I} C_i \]

Эта точка должна лежать либо в \( U \), либо в \( V \), но не в обоих одновременно, поскольку \( U \) и \( V \) образуют разделение множества \( C \). Пусть, без ограничения общности,

\[ x \in U \quad \text{и} \quad x \notin V \]

Так как каждое множество \( C_i \subset C \), имеем:

\[ C_i = (C_i \cap U) \cup (C_i \cap V) \]

Множества \( C_i \cap U \) и \( C_i \cap V \) открыты в индуцированной топологии на \( C_i \), не пересекаются и в совокупности покрывают \( C_i \). Поскольку каждое множество \( C_i \) по предположению является связным, одно из этих двух множеств должно быть пустым.

Следовательно, каждое множество \( C_i \) целиком содержится либо в \( U \), либо в \( V \):

\[ C_i \subset U \quad \text{или} \quad C_i \subset V \]

Но если \( x \in C_i \) и одновременно \( x \in U \), то невозможно, чтобы \( C_i \subset V \).

Отсюда следует, что:

\[ C_i \subset U \quad \text{для всех } i \in I \]

Следовательно, объединение \( C \) содержится в \( U \):

\[ \bigcup_{i \in I} C_i \subset U \]

Это противоречит предположению о том, что \( V \cap C \neq \varnothing \).

Полученное противоречие показывает, что исходное предположение неверно. Следовательно, объединение \( \bigcup_{i \in I} C_i \) является связным множеством.