Любое связное подмножество содержится в одной из компонент связности
Пусть \( A \) и \( B \) являются подмножествами топологического пространства \( X \). Предположим, что множество \( A \) связно и что выполняется включение \( A \subset B \). Если множество \( B \) допускает разбиение в пространстве \( X \) на два подмножества \( B_1 \) и \( B_2 \), то множество \( A \) целиком содержится ровно в одном из них: $$ A \subset B_1 \quad \text{или} \quad A \subset B_2 $$
Иными словами, связное множество не может одновременно затрагивать обе части разбиения.
Если связное множество находится внутри множества, которое распадается на два непересекающихся подмножества, то оно обязательно полностью лежит в одном из них.
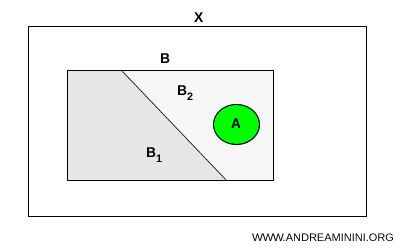
На интуитивном уровне связное множество удобно представлять как цельный кусок веревки, помещенный внутрь конверта. Если конверт разделить на два изолированных отделения, при этом веревка остается целой, то она неизбежно окажется полностью в одном из них. Иначе веревку пришлось бы разорвать. Связность именно и выражает эту идею целостности, не позволяя множеству «перешагивать» через разбиение.
Конкретный пример
Рассмотрим в качестве топологического пространства вещественную прямую:
$$ X = \mathbb{R} $$
и следующее подмножество пространства \( X \):
$$ B = (-3,4) $$
Это множество можно разложить на два подмножества:
$$ B_1 = (-3,0) $$
$$ B_2 = (0,4) $$
Эти подмножества не пересекаются:
$$ B_1 \cap B_2 = \varnothing $$
и их объединение в точности совпадает с множеством \( B \):
$$ B_1 \cup B_2 = B $$
Кроме того, множества \( B_1 \) и \( B_2 \) являются открытыми в индуцированной топологии на \( B \).
Таким образом, они образуют разбиение множества \( B \) в пространстве \( X \).
Теперь рассмотрим связное подмножество множества \( B \):
$$ A = (1,2) $$
Поскольку выполняется включение \( A \subset B_2 \), множество \( A \) целиком содержится в одной из двух частей разбиения.
Замечание. Если же взять \( A = (-1,1) \), то окажется, что $$ A \cap B_1 \neq \varnothing, \qquad A \cap B_2 \neq \varnothing $$ Такая ситуация невозможна, поскольку множества \( B_1 \) и \( B_2 \) образуют разбиение множества \( B \). Связное подмножество не может быть «размазано» по обеим частям разбиения. Если бы это происходило, то само множество \( A \) допускало бы разбиение, что противоречит связности интервала \( (-1,1) \). Следовательно, проблема состоит не в связности интервала, а в невозможности его включения в \( B \) при таком разбиении.
Доказательство
Предположения
Пусть \( A \) и \( B \) являются подмножествами топологического пространства \( X \).
$$ A \subset X \quad \text{и} \quad B \subset X $$
Предположим, что выполняются следующие условия:
- \( A \) является связным множеством
- \( A \subset B \)
- \( B_1 \) и \( B_2 \) образуют разбиение множества \( B \) в пространстве \( X \)
Утверждение
Множество \( A \) целиком содержится либо в \( B_1 \), либо в \( B_2 \):
$$ A \subset B_1 \quad \text{или} \quad A \subset B_2 $$
Доказательство
По предположению множества \( B_1 \) и \( B_2 \) образуют разбиение множества \( B \) в пространстве \( X \). Это означает, что:
- \( B_1 \cap B_2 = \varnothing \)
- \( B = B_1 \cup B_2 \)
- \( B_1 \) и \( B_2 \) открыты в индуцированной топологии на \( B \)
Предположим от противного, что множество \( A \) не содержится целиком ни в \( B_1 \), ни в \( B_2 \).
$$ A \cap B_1 \neq \varnothing \qquad \text{и} \qquad A \cap B_2 \neq \varnothing $$
Так как \( A \subset B \), имеем:
$$ A = A \cap (B_1 \cup B_2) = (A \cap B_1) \cup (A \cap B_2) $$
Множества \( A \cap B_1 \) и \( A \cap B_2 \) непусты, не пересекаются и открыты в индуцированной топологии на \( A \).
Следовательно, они образуют разбиение множества \( A \), что противоречит предположению о его связности.
Полученное противоречие показывает, что исходное предположение неверно. Тем самым доказано, что
$$ A \subset B_1 \quad \text{или} \quad A \subset B_2 $$
Доказательство завершено.
И так далее.