Теорема: характеристика связных пространств через открытые и замкнутые (клопен) множества

Топологическое пространство \( X \) называется связным тогда и только тогда, когда единственные его подмножества, которые одновременно являются открытыми и замкнутыми (клопен), - это всё пространство \( X \) и пустое множество \( \emptyset \).

Проще говоря, если в пространстве нет собственных непустых множеств, которые были бы и открытыми, и замкнутыми, значит пространство связно. Это и есть суть критерия связности.

Теорема показывает, что наличие хотя бы одного «особого» множества, которое открыто и замкнуто одновременно, разбивает пространство на две независимые части, и связь между ними теряется.

Интуиция и смысл

В топологии подмножество, которое одновременно открыто и замкнуто, фактически разделяет пространство на две части, не соединённые непрерывно.

Если такое множество существует, пространство можно разложить на два непересекающихся открытых множества. Между ними уже нет пути, который бы позволял пройти из одной части в другую без «разрыва».

В этом случае пространство несвязно.

Если же единственные клопен-множества - это всё пространство и пустое множество, то никакого разделения быть не может. Пространство остаётся связным.

Важно. В любом топологическом пространстве и всё множество \( X \), и пустое множество \( \emptyset \) всегда являются одновременно открытыми и замкнутыми. Это универсальное свойство.

Пример 1. Пространство, где связь теряется

Возьмём множество \( X = \{ a, b, c, d \} \) с топологией \( T \), где открытые множества заданы так: \( \{ b \}, \{ a, b \}, \{ c, d \}, \{ b, c, d \}, \{ a, b, c, d \}, \emptyset \).

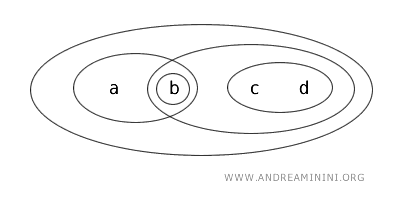
В этом пространстве подмножество \( \{ a, b \} \) - клопен. Оно открыто, потому что указано в топологии \( T \), и замкнуто, потому что его дополнение \( \{ c, d \} \) тоже открыто.

Таким образом, пространство \( (X, T) \) несвязно: уже одно такое множество показывает, что пространство можно разбить на две изолированные области - \( \{ a, b \} \) и \( \{ c, d \} \).

Пример 2. Реальная прямая без разрывов

Рассмотрим множество действительных чисел \( \mathbb{R} \) со стандартной топологией, то есть с открытыми интервалами \( (a, b) \) в качестве базовых множеств.

Интервалы \( (a, b) \) открыты, но не замкнуты, а интервалы \( [a, b] \) - замкнуты, но не открыты. Здесь нет множеств, которые одновременно и открыты, и замкнуты, кроме всего пространства \( \mathbb{R} \) и пустого множества \( \emptyset \).

Следовательно, действительная прямая со стандартной топологией является связным пространством.

Пример 3. Два отдельных отрезка

Теперь рассмотрим подпространство \( X = (0,1) \cup (2,3) \subset \mathbb{R} \) с топологией, индуцированной стандартной топологией на \( \mathbb{R} \).

Здесь интервалы \( (0,1) \) и \( (2,3) \) одновременно открыты и замкнуты в \( X \), потому что каждый из них является дополнением другого в этом подпространстве.

• Дополнение множества \( (0,1) \) в \( X \) - это \( (2,3) \), открытое в \( X \).
• Дополнение множества \( (2,3) \) в \( X \) - это \( (0,1) \), также открытое в \( X \).

Оба множества - клопен. Следовательно, подпространство \( X \) несвязно.

Несвязность возникает потому, что \( X \) можно представить как объединение двух непересекающихся непустых открытых множеств \( (0,1) \) и \( (2,3) \), которые полностью покрывают всё пространство, но между ними нет непрерывного перехода.