Связные пространства в топологии
Определение через открытые множества
Топологическое пространство $ X $ называется связным, если его невозможно разбить на два непустых, непересекающихся открытых множества $ U $ и $ V $, объединение которых даёт всё пространство $ X $.
- $ U \neq \emptyset $ и $ V \neq \emptyset $ - оба множества содержат хотя бы одну точку;
- $ U \cap V = \emptyset $ - у них нет общих элементов;
- $ U \cup V \ne X $ - вместе они не покрывают всё пространство.
Если же такие множества существуют, пространство называют несвязным.
Проще говоря, пространство считается связным, если его нельзя «разрезать» на две открытые части, не оставив ничего между ними. Если такой «разрез» возможен, пространство теряет связность.
Пара $ (U, V) $, которая разделяет пространство на такие области, называется разделением.
Замечание. Это определение топологической связности через открытые множества. Далее мы увидим, что это понятие не совпадает с «связностью по пути» - они могут описывать совершенно разные ситуации.
Разберём пример
Пусть есть множество $ X $, состоящее из трёх элементов:
$$ X = {a, b, c} $$
На этом множестве можно задать разные топологии, то есть разные способы определять, какие подмножества считаются «открытыми».
- Топология A
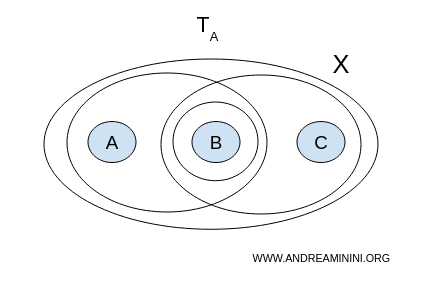
Открытые множества: $$ \mathcal{T}_A = \{ \emptyset, X, \{ a,b \}, \{ b \}, \{ b,c \} \} $$ - Топология B
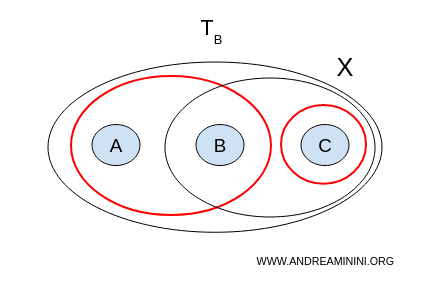
Открытые множества: $$ \mathcal{T}_B = \{ \emptyset, X, \{ a,b \}, \{ c \}, \{ b,c \} \} $$
Попробуем понять, в каком из этих случаев пространство остаётся связным.
1] Топология A
Проверим, можно ли разбить пространство $ X $ на два непересекающихся открытых множества, которые вместе образуют всё пространство.
- $ U = {a,b}, V = {b,c} $ - пересекаются по элементу $ b $;
- $ U = {a,b}, V = {b} $ - пересекаются;
- $ U = {b}, V = {b,c} $ - тоже пересекаются.
Подходящей пары не нашлось - значит, пространство с топологией A связно.
2] Топология B
Теперь рассмотрим вторую топологию:
- $ U = {a,b}, V = {b,c} $ - пересекаются по элементу $ b $;
- $ U = {a,b}, V = {c} $ - непересекающиеся, непустые множества, и их объединение даёт всё пространство $ X $.
Пара $ (U = {a,b}, V = {c}) $ действительно разделяет пространство. Значит, с топологией B пространство $ X $ - несвязно.
Замечание. Этот пример показывает, что связность зависит не только от множества точек, но и от выбранной топологии. Одинаковое множество может быть связным в одной топологии и несвязным в другой.
Пример с числовой прямой
Рассмотрим множество
$$ X = (-\infty, n) \cup (n, +\infty) $$
где $ n $ - фиксированное действительное число (например, $ n = 0 $). Это обычная числовая прямая, но без одной точки:
$$ X = \mathbb{R} \setminus {n} $$
Множества $ U = (-\infty, n) $ и $ V = (n, +\infty) $:
- открыты в стандартной топологии на $ \mathbb{R} $;
- не пересекаются;
- и оба непусты.
Их объединение даёт всё $ X $, поэтому это классический пример несвязного пространства.
Комментарий. Если удалить одну точку с числовой прямой, она «разрывается» на две независимые части - левую и правую от $ n $. Между ними больше нельзя провести непрерывный путь. Поэтому такое пространство не только несвязно, но и не является связным по пути.
Связность и связность по пути
Важно различать два понятия - топологическая связность и связность по пути.
- Топологическая связность: пространство нельзя разделить на два непересекающихся непустых открытых множества.
- Связность по пути: любые две точки можно соединить непрерывным путём, полностью лежащим внутри пространства. Если путь нигде не проходит дважды через одну точку, пространство называют связным по дуге.
Каждое связное по пути пространство всегда топологически связно, но не наоборот. Связность по пути - более сильное условие.
Если между точками существует непрерывный путь, пространство нельзя «разрезать» на отдельные части. Однако возможны и такие примеры, где пространство остаётся связным, хотя никакого пути между точками провести нельзя.
Пример. Классический случай - синусоида тополога: $$ S = { (x, \sin(1/x)) \mid x > 0 } \cup { (0, y) \mid -1 \le y \le 1 } $$ Это пространство связно, потому что его нельзя разделить на две открытые непересекающиеся части, но оно не связано по пути: не существует непрерывного пути, соединяющего точку на колеблющейся кривой с точкой на вертикальном отрезке.
Связность и связность по пути - фундаментальные понятия топологии, которые помогают понять, как устроено пространство и как части в нём «держатся вместе».
Примечания
Дополнительные сведения о связных топологических пространствах
- Теорема: характеристика связных пространств через открытые и замкнутые (клопен) множества
Топологическое пространство \( X \) является связным тогда и только тогда, когда единственными его подмножествами, одновременно открытыми и замкнутыми (клопен), являются всё пространство \( X \) и пустое множество \( \emptyset \).
И другие связанные результаты.