Разделение множества открытыми множествами

Пусть $ A $ является подмножеством топологического пространства $ X $. Говорят, что открытые множества $ U $ и $ V $ разделяют $ A $, если выполняются три условия:

$ A $ полностью содержится в объединении $ U $ и $ V $ \[ A \subseteq U \cup V \]
каждое из этих множеств пересекается с $ A $ непустым образом \[ U \cap A \neq \varnothing \] \[ V \cap A \neq \varnothing \]
их пересечение не содержит ни одной точки из $ A $ \[ U \cap V \cap A = \varnothing \]

Иначе говоря, множество $ A $ распадается на две непересекающиеся части. Одна часть находится внутри $ U $, другая внутри $ V $, и внутри самого $ A $ они не пересекаются. Это простой и наглядный способ описать ситуацию, когда подмножество оказывается разделённым топологически.

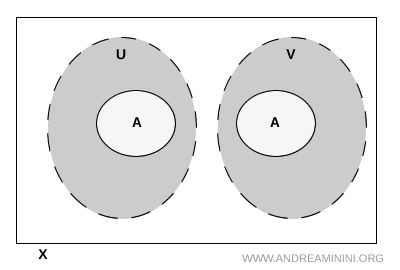
diagram illustrating the separation of a subset by open sets

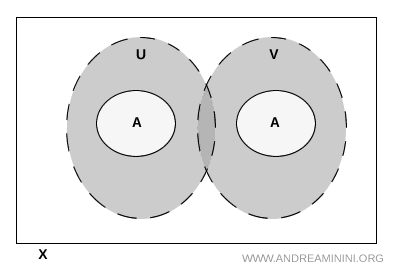
Примечание. Важно понимать, что $ U $ и $ V $ могут пересекаться во всём пространстве $ X $. Такое пересечение допустимо, если оно не затрагивает точки множества $ A $.
diagram showing that U and V may intersect outside the subset A

Пример из действительных чисел

Рассмотрим пространство $ X = \mathbb{R} $ со стандартной топологией. Пусть множество $ A $ состоит из двух раздельных замкнутых отрезков:

$$ A = [-2,-1] \cup [1,2] $$

Выберем два открытых множества, которые будут кандидатами на разделение:

$$ U = (-3,0) $$

$$ V = (0,3) $$

На рисунке ниже видно, как расположены $ A $, $ U $ и $ V $:

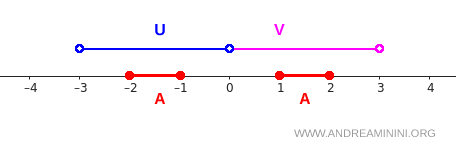
graph of the open sets U and V together with the subset A

Легко проверить, что условия разделения выполнены.

Отрезок $ [-2,-1] $ полностью лежит в $ U $.

Отрезок $ [1,2] $ полностью лежит в $ V $.

Следовательно:

$$ A \subseteq U \cup V $$

Каждое открытое множество имеет непустое пересечение с $ A $:

$$ U \cap A = [-2,-1] \neq \varnothing $$

$$ V \cap A = [1,2] \neq \varnothing $$

И, что важно, $ U $ и $ V $ не пересекаются в пределах множества $ A $:

$$ U \cap V \cap A = \varnothing $$

Таким образом, $ U $ и $ V $ действительно образуют разделение множества $ A $ в пространстве $ X $. Это классический пример, который часто используют для иллюстрации понятия разделённости в общей топологии.