Как понять, что множество несвязно: простой критерий через открытые подмножества
Пусть \(X\) топологическое пространство и \(A \subset X\). Множество \(A\) считается несвязным, если существуют два открытых множества \(U\) и \(V\) в \(X\), для которых выполняются условия:
- \(A \subset U \cup V\)
- \(U \cap A \neq \varnothing\)
- \(V \cap A \neq \varnothing\)
- \((U \cap V) \cap A = \varnothing\)
Фактически это означает, что множество можно разделить на две открытые области пространства, каждая из которых содержит часть \(A\), но внутри самого множества они не пересекаются. Такой подход даёт удобный и наглядный инструмент для выявления несвязности.
Главное достоинство критерия в том, что он опирается только на открытые множества пространства. Чтобы понять несвязность, не нужно разбираться с путями, кривыми или другими более сложными объектами.
Пример 1: два отрезка на прямой
Возьмём множество:
$$ A = [0,1] \cup [2,3] \subset \mathbb{R} $$
Это два непересекающихся замкнутых интервала. Между ними есть разрыв, и ясно, что, оставаясь внутри \(A\), нельзя перейти из одного интервала в другой.
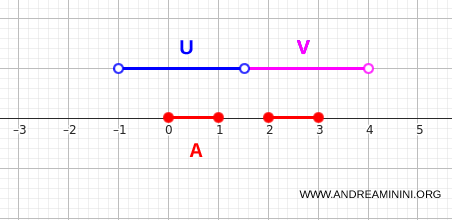
Чтобы формально подтвердить несвязность, выберем открытые множества:
- \(U = (-1,1.5)\)
- \(V = (1.5,4)\)
Тогда:
$$ U \cap A = [0,1], \qquad V \cap A = [2,3], \qquad (U \cap V) \cap A = \varnothing $$
Каждая часть множества попадает в свою открытую область, и внутри \(A\) они не соприкасаются. Это и есть несвязность.
Пример 2: две изолированные точки
Теперь рассмотрим совсем простое множество:
$$ A = \{1, 3\} \subset \mathbb{R} $$
Точки находятся далеко друг от друга и никак не связаны внутри самого множества.
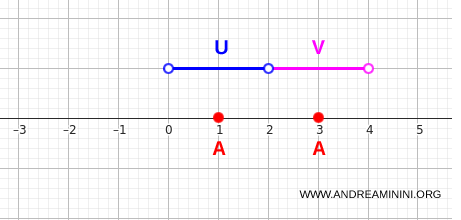
Подойдут такие открытые множества:
$$ U = (0,2), \qquad V = (2,4) $$
Тогда:
$$ U \cap A = \{1\}, \qquad V \cap A = \{3\}, \qquad U \cap V \cap A = \varnothing $$
Точки разделяются естественным образом. Множество несвязно.
Пример 3: два полупространства в \(\mathbb{R}^2\)
Рассмотрим плоскость без оси \(x\):
$$ A = \{(x,y) : y>0\} \cup \{(x,y) : y<0\} $$
Перед нами верхнее и нижнее полупространства. Они открыты и отделены друг от друга прямой \(y = 0\), которая в множество не входит.
Выберем:
$$ U = \{(x,y) : y> -1\}, \qquad V = \{(x,y) : y< 1\} $$
- \(U \cap A\) содержит весь верхний слой,
- \(V \cap A\) содержит весь нижний слой.
Так как точки \(A\) не попадают в пересечение \(U\) и \(V\), множество несвязно.
Как устроено доказательство
Критерий работает в обе стороны, что делает его особенно мощным.
A] Если множество можно разделить открытыми областями, оно несвязно
Пусть найдены открытые множества \(U\) и \(V\). Обозначим:
\[ P = U \cap A, \qquad Q = V \cap A \]
Тогда:
- \(P\) и \(Q\) непусты,
- открыты в топологии подпространства,
- не пересекаются,
- покрывают всё множество \(A\).
То есть они образуют стандартное разделение множества. Значит, \(A\) несвязно.
B] Если множество несвязно, открытые области обязательно найдутся
Пусть \(A\) несвязно и пусть его разделяют подмножества \(P\) и \(Q\). Поскольку они открыты в подпространстве, существуют открытые множества \(U\) и \(V\) в \(X\), такие что:
\[ P = U \cap A, \qquad Q = V \cap A. \]
Остаётся заметить, что \(U\) и \(V\) автоматически выполняют условия критерия.
C] Итог
Множество \(A\) несвязно тогда и только тогда, когда его можно разложить на две непересекающиеся открытые части, возникающие как пересечения с открытыми множествами пространства \(X\). Это простой, прозрачный и почти всегда удобный способ увидеть структуру множества через его взаимодействие с открытыми областями.